题目内容
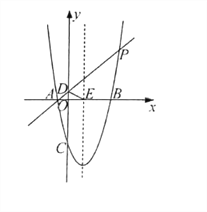
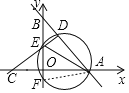
【题目】如图,在平面内直角坐标系中,直线y=-x+6分别于x轴、y轴交于A、B两点,点C与点A关于y轴对称,点E为线段OB上一动点(不与O、B重合),CE的延长线与AB交于点D,过A、D、E三点的圆与y轴交于点F
(1)求A、B、C三点的坐标
(2)求证:BE·EF=DE·AE
(3)若tan∠BAE=![]() ,求点F的坐标
,求点F的坐标
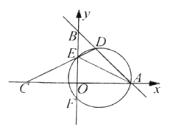
【答案】(1) A(6,0);B(0,6);C(-6,0);(2)见解析;(3)(0,-2).
【解析】分析:(1)利用直线y=-x+6可求得A、B的坐标,再利用对称可求得C点坐标;
(2)连接AF,可证得△BED∽△AEF,利用相似三角形的性质可证得结论;
(3)利用(2)中三角形相似,结合条件可求得∠BAE=∠FAO,在Rt△AOF中,利用三角函数定义可求得OF的长,则可求得F点的坐标.
详解:(1)在y=-x+6中,令y=0可得x=6,令x=0可得y=6,
∴A(6,0),B(0,6),
∵点C与A关于y轴对称,
∴C(-6,0);
(2)连接AF,由(1)可知OC=OA,
在△COE和△AOE中
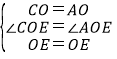 ,
,
∴△COE≌△AOE(SAS),
∴∠CEO=∠AEO,
∵∠CEO=∠BED,
∴∠BED=∠AEO,
∵四边形ADEF内接于圆,
∴∠BDE=∠EFA,
∴△BED∽△AEF,
∴![]() ,
,
∴BEEF=DEAE;
(3)∵△BED∽△AEF,
∴∠EAF=∠EBD,
∵OA=OB=6,∠AOB=90°,
∴∠ABO=∠OAB=45°,
∴∠EAF=45°,
∴∠BAE+∠EAO=∠FAO+∠EAO=45°,
∴∠BAE=∠FAO,
∴tan∠FAO=tan∠BAE=![]() ,
,
∴![]() ,
,
∵OA=6,
∴OF=2,
∴F(0,-2).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】从谢家集到田家庵有3路,121路,26路三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从谢家集到田家庵的用时时间,在每条线路上随机选取了450个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:早高峰期间,乘坐______(填“3路”,“121路”或“26路”)线路上的公交车,从谢家集到田家庵“用时不超过50分钟”的可能性最大.
用时 |
|
|
| 合计(频次) |
线路 | ||||
3路 | 260 | 167 | 23 | 450 |
121路 | 160 | 166 | 124 | 450 |
26路 | 50 | 122 | 278 | 450 |
【题目】学生小明、小华为了解本校八年级学生每周上网的时间,各自进行了抽样调查.小明调查了八年级信息技术兴趣小组中40名学生每周上网的时间,算得这些学生平均每周上网时间为2.5h;小华从全体320名八年级学生名单中随机抽取了40名学生,调查了他们每周上网的时间,算得这些学生平均每周上网时间为1.2h.小明与小华整理各自样本数据,如表所示.
时间段(h/周) | 小明抽样人数 | 小华抽样人数 |
0~1 | 6 | 22 |
1~2 | 10 | 10 |
2~3 | 16 | 6 |
3~4 | 8 | 2 |
(每组可含最低值,不含最高值)
请根据上述信息,回答下列问题:
(1)你认为哪位学生抽取的样本具有代表性?_____.
估计该校全体八年级学生平均每周上网时间为_____h;
(2)在具有代表性的样本中,中位数所在的时间段是_____h/周;
(3)专家建议每周上网2h以上(含2h)的同学应适当减少上网的时间,根据具有代表性的样本估计,该校全体八年级学生中有多少名学生应适当减少上网的时间?