Question

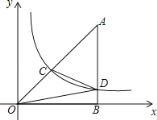
【题目】如图，△OAB中，∠ABO＝90°，点A位于第一象限，点O为坐标原点，点B在x轴正半轴上，若双曲线y＝（x＞0）与△OAB的边AO、AB分别交于点C、D，点C为AO的中点，连接OD、CD．若S△OBD＝3，则S△OCD为（　　）

A.3B.4C.D.6

Answer 1

【答案】C

【解析】

根据反比例函数关系式与面积的关系得S△COE=S△BOD=3，由C是OA的中点得S△ACD=S△COD，由CE∥AB，可知△COE∽△AOB，由面积比是相似比的平方得，求出△ABC的面积，从而求出△AOD的面积，得出结论．

解：过C作CE⊥OB于E，

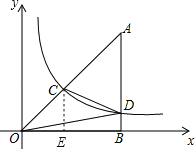
∵点C、D在双曲线y＝（x＞0）上，

∴S△COE＝S△BOD，

∵S△OBD＝3，

∴S△COE＝3，

∵CE∥AB，

∴△COE∽△AOB，

∴＝，

∵C是OA的中点，

∴OA＝2OC，

∴＝，

∴S△AOB＝4×3＝12，

∴S△AOD＝S△AOB﹣S△BOD＝12﹣3＝9，

∵C是OA的中点，

∴S△ACD＝S△COD，

∴S△COD＝，

故选：C．