题目内容
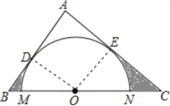
【题目】如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,以O为圆心的半圆分别与AB、AC边相切于D、E两点,且O点在BC边上,则图中阴影部分面积S阴等于( )

A. ![]() B.
B. ![]() C. 5-
C. 5-![]() D.
D. ![]()
【答案】D
【解析】分析:连接OD,OE, 设O与BC交于M、N两点,易得四边形ADOE是正方形,即可得到∠DOM+∠EON=90°,然后设OE=x,由△COE∽△CBA,根据相似三角形的对应边成比例,即可求得x的值,继而由△ABC上边的阴影部分的面积可用△BOD和△BOD内部的扇形的面积差来得出,同理可求出△ABC下边的阴影部分的面积.由此可得出所求的结果.
详解:连接OD,OE,设O与BC交于M、N两点,
∵AB、AC分别切⊙O于D、E两点,
∴∠ADO=∠AEO=90°,
又∵∠A=90°,
∴四边形ADOE是矩形,
∵OD=OE,
∴四边形ADOE是正方形,
∴∠DOE=90°,
∴∠DOM+∠EON=90°,
设OE=x,则AE=AD=OD=x,EC=AC-AE=4-x
∵△COE∽△CBA
∴![]()
∴![]()
解得x=![]()
∴S阴影=S△ABC-S正方形ADOE﹣(S扇形DOM+S扇形EON)=![]() ×3×4-(
×3×4-(![]() )2-
)2-![]() =
=![]() .
.
故选:D.

练习册系列答案
相关题目