题目内容
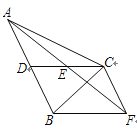
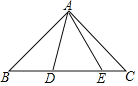
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点D,E均在边BC上,且∠DAE=45°
(1)若BD=2,CE=4,则DE=_____.
(2)若∠AEB=75°,则线段BD与CE的数量关系是______.
【答案】2![]() CE=
CE=![]() BD
BD
【解析】
(1)将△ABD绕点A逆时针旋转90°,至△ACD',则AB与AC重合,连接ED',则CD'=BD=2,∠CAD'=∠BAD,AD'=AD,∠DAD'=90°,∠ACD'=∠ABD,证明△AD'E≌△ADE(SAS),得出D'E=DE,由等腰直角三角形的性质得出∠B=∠ACB=45°,得出∠D'CE=90°,在Rt△CD'E中,由勾股定理得出D'E=![]() ,即可得出答案;
,即可得出答案;
(2)由(1)得出∠D'CE=90°,△AD'E≌△ADE,由全等三角形的性质得出D'E=DE,∠AED'=∠AEB=75°,求出∠CED'=30°,由含30°角的直角三角形的性质即可得出结论.
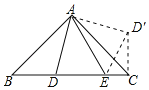
(1)将△ABD绕点A逆时针旋转90°,至△ACD',则AB与AC重合,连接ED',如图所示:
则CD'=BD=2,∠CAD'=∠BAD,AD'=AD,∠DAD'=90°,∠ACD'=∠ABD,
∵∠BAC=90°,∠DAE=45°,
∴∠D'AE=90°﹣45°=45°=∠DAE,
在△AD'E和△ADE中,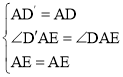 ,
,
∴△AD'E≌△ADE(SAS),
∴D'E=DE,
∵∠BAC=90°,AB=AC,
∴∠B=∠ACB=45°,
∴∠D'CE=45°+45°=90°,
在Rt△CD'E中,由勾股定理得:D'E=![]() =
=![]() =2
=2![]() ,
,
∴DE=2![]() ;
;
故答案为:2![]() ;
;
(2)CE=![]() BD,理由如下:
BD,理由如下:
由(1)得:∠D'CE=90°,△AD'E≌△ADE,
∴D'E=DE,∠AED'=∠AEB=75°,
∴∠CED'=180°﹣75°﹣75°=30°,
∴CE=![]() CD',
CD',
∴CE=![]() BD,
BD,
故答案为:CE=![]() BD.
BD.