题目内容
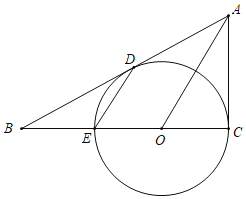
【题目】在Rt△ABC中,BC=9, CA=12,∠ABC的平分线BD交AC与点D, DE⊥DB交AB于点E.
(1)设⊙O是△BDE的外接圆,求证:AC是⊙O的切线;
(2)设⊙O交BC于点F,连结EF,求![]() 的值.
的值.
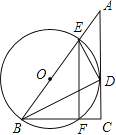
【答案】(1)见详解;
(2)![]() .
.
【解析】
(1)因为点D在⊙O上,所以只要连结圆心和圆上这点,证明OD和AC垂直即可.
利用角平分线、等腰三角形、直角三角形两锐角互余,完成证明.
(2)利用勾股定理求得AB的长.;利用△ADO∽△ACB对应线段成比例求得BE的长;利用△BEF∽△BAC得![]() =
=![]() ,从而问题得解.
,从而问题得解.
(1)证明:由已知DE⊥DB,⊙O是Rt△BDE的外接圆,
∴BE是⊙O的直径,点O是BE的中点,连结OD,
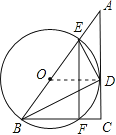
∵![]() ,∴
,∴![]() .
.
又∵BD为∠ABC的平分线,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() ,即∴
,即∴![]()
又∵OD是⊙O的半径,
∴AC是⊙O的切线.
(2) 解:设⊙O的半径为r, 在Rt△ABC中,![]() ,
,
∴![]()
∵![]() ,
,![]() ,∴△ADO∽△ACB.
,∴△ADO∽△ACB.
∴![]() .∴
.∴![]() .
.
∴![]() .∴
.∴![]()
又∵BE是⊙O的直径.∴![]() .∴△BEF∽△BAC
.∴△BEF∽△BAC
∴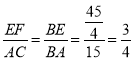 .
.

练习册系列答案
相关题目