Question

【题目】已知边长为2a的正方形ABCD，对角线AC、BD交于点Q，对于平面内的点P与正方形ABCD，给出如下定义：如果，则称点P为正方形ABCD的“关联点”.在平面直角坐标系xOy中，若A（﹣1，1），B（﹣1，﹣1），C（1，﹣1），D（1，1）.

（1）在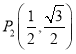，，中，正方形ABCD的“关联点”有_____；

（2）已知点E的横坐标是m，若点E在直线上，并且E是正方形ABCD的“关联点”，求m的取值范围；

（3）若将正方形ABCD沿x轴平移，设该正方形对角线交点Q的横坐标是n，直线与x轴、y轴分别相交于M、N两点.如果线段MN上的每一个点都是正方形ABCD的“关联点”，求n的取值范围.

Answer 1

【答案】（1）正方形ABCD的“关联点”为P2，P3；（2）或；（3）.

【解析】

（1）正方形ABCD的“关联点”中正方形的内切圆和外切圆之间（包括两个圆上的点），由此画出图形即可判断；

（2）因为E是正方形ABCD的“关联点”，所以E在正方形ABCD的内切圆和外接圆之间（包括两个圆上的点），因为E在直线上，推出点E在线段FG上，求出点F、G的横坐标，再根据对称性即可解决问题；

（3）因为线段MN上的每一个点都是正方形ABCD的“关联点”，分两种情形：①如图3中，MN与小⊙Q相切于点F，求出此时点Q的横坐标；②M如图4中，落在大⊙Q上，求出点Q的横坐标即可解决问题；

（1）由题意正方形ABCD的“关联点”中正方形的内切圆和外切圆之间（包括两个圆上的点），

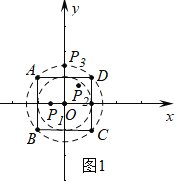
观察图象可知：正方形ABCD的“关联点”为P2，P3；

（2）作正方形ABCD的内切圆和外接圆，

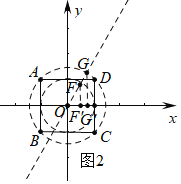
∴OF＝1，，.

∵E是正方形ABCD的“关联点”，

∴E在正方形ABCD的内切圆和外接圆之间（包括两个圆上的点），

∵点E在直线上，

∴点E在线段FG上.

分别作FF’⊥x轴，GG’⊥x轴，

∵OF＝1，，

∴，.

∴.

根据对称性，可以得出.

∴或.

（3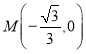）∵、N（0，1），

∴，ON＝1.

∴∠OMN＝60°.

∵线段MN上的每一个点都是正方形ABCD

的“关联点”，

①MN与小⊙Q相切于点F，如图3中，

∵QF＝1，∠OMN＝60°，

∴.

∵，

∴.

∴.

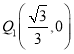②M落在大⊙Q上，如图4中，

∵，，

∴.

∴.

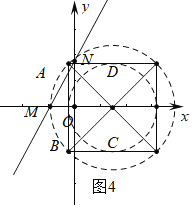
综上：.