��Ŀ����
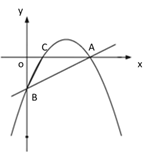
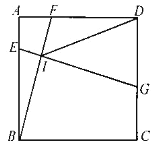
����Ŀ����֪������y��ax2+bx+c(a��0)�Ķ���M(1����4a)���ҹ���A(4��t)����x�ύ��B��C����(��B�ڵ�C�����)��ֱ��l������A��B����y�ύ�ڵ�D.
(1)��a����1����2��x��4ʱ����y�ķ�Χ��
(2)����MBC�ǵ���ֱ�������Σ����ABM�������
(3)��E��ֱ��l�Ϸ����������ϵĶ��㣬��BDE����������ֵΪ![]() ����P�������ߵĶԳ����ϵ�һ�㣬��Q���������ϣ��Ե�A��B��P��QΪ������ı����ܷ�Ϊ���Σ����ܣ������P�����ꣻ�����ܣ���˵������.
����P�������ߵĶԳ����ϵ�һ�㣬��Q���������ϣ��Ե�A��B��P��QΪ������ı����ܷ�Ϊ���Σ����ܣ������P�����ꣻ�����ܣ���˵������.
���𰸡�(1) ��5��y��3��(2)��ABM�������4��(3)�Ե�A��D��P��QΪ�����ƽ���ı��ζ��������Ǿ��Σ����ɼ�����.
��������
(1)a����1ʱ��y����(x��3)(x+1)����x��2ʱ��y��3����x��4ʱ��y����5��������⣻
(2)��MBC�ǵ���ֱ�������Σ���yM��![]() BC��2����ABM�������
BC��2����ABM�������![]() ��CB��yM��
��CB��yM��![]() ��4��2��4��
��4��2��4��
(3)S��ACE��S��AFE��S��CFE�����a����1����AD��ƽ���ı��ε�һ���ߡ�AD��ƽ���ı��ε�һ���Խ��ߣ��ֱ���⼴��.
�⣺y��a(x��1)2��4a��ax2��2ax��3a��
��y��0����0��ax2��2ax��3a��
���x1����1��x2��3
�ߵ�A�ڵ�B����࣬
��A(��1��0)��
��ֱ��l������A��
��0����k+b��b��k��
��y��kx+k��
�ߵ�D�ĺ�����Ϊ4����ax2��2ax��3a��kx+k��
��a��42��2a��4��3a��k��4+k��
��k��a��
��ֱ��l�ĺ�������ʽΪy��ax+a��
(1)a����1ʱ��y����(x��3)(x+1)��
��x��2ʱ��y��3����x��4ʱ��y����5��
�ʩ�5��y��3��
(2)��MBC�ǵ���ֱ�������Σ���yM��![]() BC��2��
BC��2��
��ABM�������![]() ��CB��yM��
��CB��yM��![]() 4��2��4��
4��2��4��
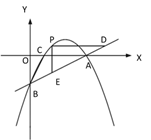
(3)���ͼ1������E��EF��y�ᣬ��ֱ��l�ڵ�F��
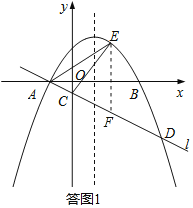
��E(x��ax2��2ax��3a)����F(x��ax+a)
EF��ax2��2ax��3a��(ax+a)��ax2��3ax��4a
S��ACE��S��AFE��S��CFE
��![]() (ax2��3ax��4a)(x+1)��
(ax2��3ax��4a)(x+1)��![]() (ax2��3ax��4a)x
(ax2��3ax��4a)x
��![]() (ax2��3ax��4a)��
(ax2��3ax��4a)��![]() a(x��
a(x��![]() )2��
)2��![]() a��
a��
���ACE����������ֵΪ��![]() a��
a��
�ߡ�ACE����������ֵΪ![]() ��
��
�ੁ![]() a��
a��![]() ��
��
���a����1��
�����߽���ʽΪy����x2+2x+3��
��A(��1��0)��D(4����5)��
��A��D���������5��
�������ߵĶԳ���Ϊx��1��
��P��������1��
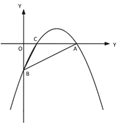
�����ͼ2����AD��ƽ���ı��ε�һ���ߣ�AD��QP�����P���Q�ĺ��������5����Q��������ǩ�4��

��Q(��4����21)��
�����ͼ3����AD��ƽ���ı��ε�һ���Խ��ߣ�
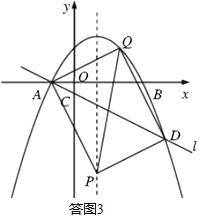
���߶�AD���е�ĺ�������![]() ��
��
��P��������1��
��Q���������2��
��Q(2��3)��
����֤���������Ե�A��D��P��QΪ�����ƽ���ı��ζ��������Ǿ���.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д� Ŀ�����ϵ�д�
Ŀ�����ϵ�д�����Ŀ������ij�����ڡ�����ƶ���������ũ��Ʒ��������������������![]() (������·�
(������·�![]() (��)�Ĺ�ϵΪ:
(��)�Ĺ�ϵΪ: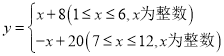
ÿ����Ʒ������![]() (Ԫ)���·�
(Ԫ)���·�![]() (��)�Ĺ�ϵ���±�:
(��)�Ĺ�ϵ���±�:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 10 | 10 |
![]() ������ݱ���ֱ��д��ÿ����Ʒ����z (Ԫ) ���·�
������ݱ���ֱ��д��ÿ����Ʒ����z (Ԫ) ���·�![]() (��)�ĺ�����ϵʽ;
(��)�ĺ�����ϵʽ;
![]() ��������
��������![]() (��Ԫ) =����������
(��Ԫ) =����������![]() (���)
(���) ![]() ����ÿ����Ʒ������
����ÿ����Ʒ������![]() (Ԫ)����������
(Ԫ)����������![]() (��Ԫ)���·�
(��Ԫ)���·�![]() (��)�Ĺ�ϵʽ;
(��)�Ĺ�ϵʽ;
![]() ��
��![]() Ϊ��ֵʱ��������
Ϊ��ֵʱ��������![]() �����ֵ�����ֵΪ����?
�����ֵ�����ֵΪ����?
����Ŀ��Ϊ�˽�ij��������ɫ���С���ʽ�������ijУ��ѧ��ȤС�����ʾ��������ʽ�����������ij�в��ֳ����������Ҫ���з�ʽ�������ʾ����������ֻ���������������ѡ��һ�ࣩ���������������Ƴ����²�������ͳ��ͼ��
���� | A | B | C | D | E |
���з�ʽ | �������� | ���� | ������ | ��ʿ | ˽�ҳ� |
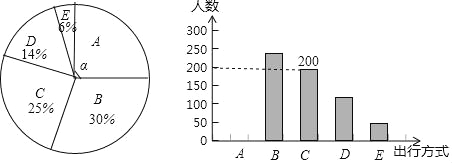
����������Ϣ���ش��������⣺
��1�����뱾���ʾ������������ �ˣ�����ѡ��B��������� �ˣ�
��2��������ͳ��ͼ�У���A���Ӧ����Բ�ĽǦ��Ķ���������ȫ����ͳ��ͼ��
��3������Լ��12���˳��У�����A��B��C��������з�ʽ����Ϊ����ɫ���С���ʽ������Ƹ��С���ɫ���С���ʽ��������