题目内容
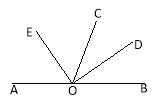
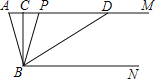
【题目】如图, BD 是△ABC 的角平分线, AE⊥ BD ,垂足为 F ,若∠ABC=35°,∠ C=50°,则∠CDE 的度数为( )

A.35°B.40°C.45°D.50°
【答案】C
【解析】
根据角平分线的定义和垂直的定义得到∠ABD=∠EBD=![]() ∠ABC=
∠ABC=![]() ,∠AFB=∠EFB=90°,推出AB=BE,根据等腰三角形的性质得到AF=EF,求得AD=ED,得到∠DAF=∠DEF,根据三角形的外角的性质即可得到结论.
,∠AFB=∠EFB=90°,推出AB=BE,根据等腰三角形的性质得到AF=EF,求得AD=ED,得到∠DAF=∠DEF,根据三角形的外角的性质即可得到结论.
∵BD是△ABC的角平分线,AE⊥BD,
∴∠ABD=∠EBD=![]() ∠ABC=
∠ABC=![]() ,∠AFB=∠EFB=90°,
,∠AFB=∠EFB=90°,
∴∠BAF=∠BEF=90°-17.5°,
∴AB=BE,
∴AF=EF,
∴AD=ED,
∴∠DAF=∠DEF,
∵∠BAC=180°-∠ABC-∠C=95°,
∴∠BED=∠BAD=95°,
∴∠CDE=95°-50°=45°,
故选C.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
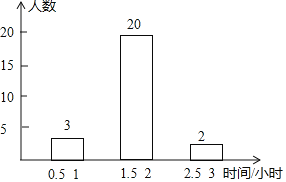
【题目】某校七年级开展了为期一周的“敬老爱亲”社会活动,并根据学生做家务的时间来评价他们在活动中的表现,学校随机抽查了部分学生在这次活动中做家务的时间,并绘制了如下的频数分布表和频数分布直方图.请根据图表中提供的信息,解答下列问题:
等级 | 做家务时间(小时) | 频数 | 百分比 |
A | 0.5≤x<1 | 3 | 6% |
B | 1<x<1.5 | a | 30% |
C | 1.5≤x<2 | 20 | 40% |
D | 2≤x<2.5 | b | m |
E | 2.5≤x<3 | 2 | 4% |
(1)这次活动中抽查的学生有______人,表中a=______,b=______,m=______,并补全频数分布直方图;
(2)若该校七年级有700名学生,请估计这所学校七年级学生一周做家务时间不足2小时而又不低于1小时的大约有多少人?