题目内容
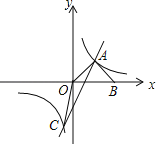
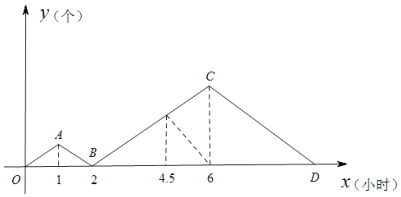
【题目】甲,乙两人同时各接受了300个零件的加工任务,甲比乙每小时加工的数量多,两人同时开工,其中一人因机器故障停止加工若干小时后又继续按原速加工,直到他们完成任务。如图表示甲比乙多加工的零件数量y(个)与加工时间x(小时)之间的函数关系,观察图象解决下列问题:

(1)其中一人因故障,停止加工_________小时,C点表示的实际意义是________________.甲每小时加工的零件数量为_____________个;
(2)求线段BC对应的函数关系式和D点坐标;
(3)乙在加工的过程中,多少小时时比甲少加工75个零件?
(4)为了使乙能与甲同时完成任务,现让丙帮乙加工,直到完成.丙每小时能加工80个零件,并把丙加工的零件数记在乙的名下,问丙应在第多少小时时开始帮助乙?并在图中用虚线画出丙帮助后y与x之间的函数关系的图象.
【答案】(1)1,![]() 点表示的实际意义是:甲工作6小时后完成任务,60;(2)
点表示的实际意义是:甲工作6小时后完成任务,60;(2)![]() 函数关系式:
函数关系式:![]() ,
,![]() ;(3)4.5或7.5小时;(4)4.5小时,见解析.
;(3)4.5或7.5小时;(4)4.5小时,见解析.
【解析】
(1)根据函数图象可以解答本题;
(2)根据题意和函数图象可以求得点C的坐标,从而可以求得线段BC对应的函数解析式;
(3)根据题意和图象可知它们相差75个零件在BC段和CD段,从而可以解答本题;
(4)根据题意和图象可以求得丙应在第多少小时时开始帮助乙,并在图中用虚线画出丙帮助后y与x之间的函数关系的图象.
解:(1)由题意可得,
其中一人因故障,停止加工2-1=1小时,C点表示的实际意义是甲工作6小时完成任务,甲每小时加工的零件数量为:300÷(6-1)=60个,
故答案为:1、甲工作6小时完成任务、60;
(2)设线段BC对应的函数关系式y=kx+b,
点C的纵坐标是:300-60÷2×6=120,
∴点C的坐标是(6,120)
![]() ,得
,得![]() ,
,
即线段BC对应的函数关系式y=30x-60,
点D的横坐标为:300÷(60÷2)=10,
故点D的坐标为(10,0);
(3)当y=75时,75=30x-60,得x=4.5,
当在CD段时,当乙比甲少加工75个零件时的时间为:(300-75)÷30=7.5(小时),
即当在4,5小时或7.5小时时,乙在加工的过程中,比甲少加工75个零件;
(4)由题意可得,
当x=6时,y=30×6-60=120,
120÷80=1.5,
∴丙应在第4.5小时时开始帮助乙,图象如图所示.

【题目】我市某乡镇在“精准扶贫”活动中销售农产品,经分析发现月销售量![]() (万件与月份
(万件与月份![]() (月)的关系为:
(月)的关系为: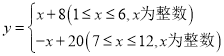
每件产品的利润![]() (元)与月份
(元)与月份![]() (月)的关系如下表:
(月)的关系如下表:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 10 | 10 |
![]() 请你根据表格直接写出每件产品利润z (元) 与月份
请你根据表格直接写出每件产品利润z (元) 与月份![]() (月)的函数关系式;
(月)的函数关系式;
![]() 若月利润
若月利润![]() (万元) =当月销售量
(万元) =当月销售量![]() (万件)
(万件) ![]() 当月每件产品的利润
当月每件产品的利润![]() (元),求月利润
(元),求月利润![]() (万元)与月份
(万元)与月份![]() (月)的关系式;
(月)的关系式;
![]() 当
当![]() 为何值时,月利润
为何值时,月利润![]() 有最大值,最大值为多少?
有最大值,最大值为多少?