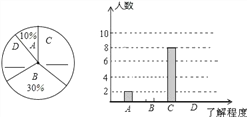
ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥ΓΑ–Υ»Λ–ΓΉιΓ±ΗυΨί―ßœΑΚ· ΐΒΡΨ≠―ιΘ§Ε‘Κ· ΐyΘΫx+![]() ΒΡΆΦœσΚΆ–‘÷ Ϋχ––ΝΥΧΫΨΩΘ§ΧΫΨΩΙΐ≥Χ»γœ¬Θ§«κ≤Ι≥δΆξ’ϊ
ΒΡΆΦœσΚΆ–‘÷ Ϋχ––ΝΥΧΫΨΩΘ§ΧΫΨΩΙΐ≥Χ»γœ¬Θ§«κ≤Ι≥δΆξ’ϊ
Θ®1Θ©Κ· ΐyΘΫx+![]() ΒΡΉ‘±δΝΩ»Γ÷ΒΖΕΈß «ΓΓ ΓΓΘ°
ΒΡΉ‘±δΝΩ»Γ÷ΒΖΕΈß «ΓΓ ΓΓΘ°
Θ®2Θ©œ¬±μ «x”κyΒΡΦΗΉιΕ‘”Π÷Β

‘ρ±μ÷–mΒΡ÷ΒΈΣΓΓ ΓΓΘ°
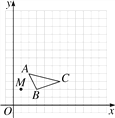
Θ®3Θ©ΗυΨί±μ÷– ΐΨίΘ§‘Ύ»γΆΦΥυ ΨΤΫΟφ÷±Ϋ«Ήχ±ξxOy÷–ΟηΒψΘ§≤ΔΜ≠≥ωΚ· ΐΒΡ“Μ≤ΩΖ÷Θ§«κΜ≠≥ωΗΟΚ· ΐΒΡΆΦœσΒΡΝμ“Μ≤ΩΖ÷Θ§
Θ®4Θ©Ιέ≤λΚ· ΐΆΦœσΘΚ–¥≥ωΗΟΚ· ΐΒΡ“ΜΧθ–‘÷ ΘΚΓΓ ΓΓΘ°
Θ®5Θ©Ϋχ“Μ≤ΫΧΫΨΩΖΔœ÷ΘΚΚ· ΐyΘΫx+![]() ΆΦœσ”κ÷±œΏyΘΫ©¹2÷Μ”–“ΜΫΜΒψΘ§Υυ“‘ΖΫ≥Χx+
ΆΦœσ”κ÷±œΏyΘΫ©¹2÷Μ”–“ΜΫΜΒψΘ§Υυ“‘ΖΫ≥Χx+![]() ΘΫ©¹2÷Μ”–1Ηω Β ΐΗυΘ§»τΖΫ≥Χx+
ΘΫ©¹2÷Μ”–1Ηω Β ΐΗυΘ§»τΖΫ≥Χx+![]() ΘΫkΘ®xΘΦ0Θ©”–ΝΫΗω≤ΜœύΒ»ΒΡ Β ΐΗυΘ§‘ρkΒΡ»Γ÷ΒΖΕΈß «ΓΓ ΓΓΘ°
ΘΫkΘ®xΘΦ0Θ©”–ΝΫΗω≤ΜœύΒ»ΒΡ Β ΐΗυΘ§‘ρkΒΡ»Γ÷ΒΖΕΈß «ΓΓ ΓΓΘ°
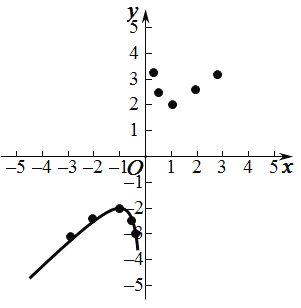
ΓΨ¥πΑΗΓΩΘ®1Θ©xΓΌ0ΘΜΘ®2Θ©![]() ΘΜΘ®3Θ©ΦϊΫβΈωΘΜΘ®4Θ©Κ· ΐΆΦœσΙΊ”Ύ‘≠ΒψΕ‘≥ΤΘΜΘ®5Θ©kΘΦ©¹2
ΘΜΘ®3Θ©ΦϊΫβΈωΘΜΘ®4Θ©Κ· ΐΆΦœσΙΊ”Ύ‘≠ΒψΕ‘≥ΤΘΜΘ®5Θ©kΘΦ©¹2
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΖ÷ Ϋ”–“β“εΒΡΧθΦΰ «Ζ÷ΡΗ≤Μ0Ν–≥ω≤ΜΒ» ΫΘ§¥”Εχ«σ≥ω![]() ΒΡ»Γ÷ΒΖΕΈßΘΜ
ΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©ΗυΨί±μ÷– ΐΨίΒΡΙφ¬…Θ§Β±![]() ±Θ§¥ζ»κΫβΈω ΫΩ…«σΒΟ
±Θ§¥ζ»κΫβΈω ΫΩ…«σΒΟ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®3Θ©ΗυΨί±μ÷– ΐΨίΘ§œ»ΟηΒψΘ§‘ΌΝ§œΏΦ¥Ω…ΒΟΒΫ≤ΩΖ÷Κ· ΐΒΡΆΦœσΘΜ
Θ®4Θ©Ιέ≤λ±μ÷– ΐΨίΚΆΚ· ΐΆΦœσΒΡΧΊ’ςΘ§–¥≥ωΤδ÷–“ΜΧθ–‘÷ Φ¥Ω…ΘΜ
Θ®5Θ©¥”ΆΦœσ…œΩ…“‘Ω¥≥ωΘ§Β±![]() ±Θ§‘Ύ÷±œΏyΘΫ©¹2ΒΡœ¬ΖΫΘ§Κ· ΐ
±Θ§‘Ύ÷±œΏyΘΫ©¹2ΒΡœ¬ΖΫΘ§Κ· ΐ![]()
![]() ΆΦœσ”κ÷±œΏ
ΆΦœσ”κ÷±œΏ![]() ”–ΝΫΗωΫΜΒψΘ§Φ¥≥Χx+
”–ΝΫΗωΫΜΒψΘ§Φ¥≥Χx+![]() ΘΫkΘ®xΘΦ0Θ©”–ΝΫΗω≤ΜœύΒ»ΒΡ Β ΐΗυΘ§Ι Ω…«σΒΟkΒΡ»Γ÷ΒΖΕΈß.
ΘΫkΘ®xΘΦ0Θ©”–ΝΫΗω≤ΜœύΒ»ΒΡ Β ΐΗυΘ§Ι Ω…«σΒΟkΒΡ»Γ÷ΒΖΕΈß.
Θ®1Θ©ΓΏ![]() ‘ΎΖ÷ΡΗ…œΘ§
‘ΎΖ÷ΡΗ…œΘ§
Γύ![]() Θ°
Θ°
Ι ¥πΑΗΈΣΘΚ![]() Θ°
Θ°
Θ®2Θ©Β±![]() ±Θ§
±Θ§![]() Θ°
Θ°
Ι ¥πΑΗΈΣΘΚ![]() ΘΜ
ΘΜ
Θ®3Θ©Ν§Βψ≥…œΏΘ§Μ≠≥ωΚ· ΐΆΦœσΘ§»γΆΦΥυ ΨΘ°
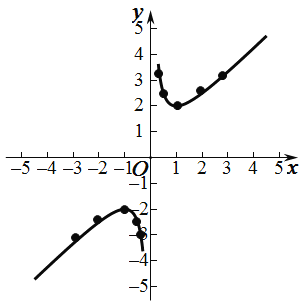
Θ®4Θ©Ιέ≤λΚ· ΐΆΦœσΘ§Ω…÷ΣΘΚΚ· ΐΆΦœσ‘Ύ“ΜΓΔ»ΐœσœό«“ΙΊ”Ύ‘≠ΒψΕ‘≥ΤΘ§
Ι ¥πΑΗΈΣΘΚΚ· ΐΆΦœσ‘Ύ“ΜΓΔ»ΐœσœό«“ΙΊ”Ύ‘≠ΒψΕ‘≥ΤΘΜ
Θ®5Θ©ΓΏΚ· ΐ![]()
![]() ΆΦœσ”κ÷±œΏyΘΫ©¹2÷Μ”–“ΜΫΜΒψΘ§Υυ“‘ΖΫ≥Χ
ΆΦœσ”κ÷±œΏyΘΫ©¹2÷Μ”–“ΜΫΜΒψΘ§Υυ“‘ΖΫ≥Χ![]()
![]() ΘΫ©¹2÷Μ”–1Ηω Β ΐΗυΘ§
ΘΫ©¹2÷Μ”–1Ηω Β ΐΗυΘ§
Γύ![]() ΘΦ0 ±Θ§ΗΟΚ· ΐΒΡΉν¥σ÷Β©¹2Θ§
ΘΦ0 ±Θ§ΗΟΚ· ΐΒΡΉν¥σ÷Β©¹2Θ§
»τΖΫ≥Χ![]()
![]() ΘΫkΘ®xΘΦ0Θ©”–ΝΫΗω≤ΜœύΒ»ΒΡ Β ΐΗυΘ§‘ρkΘΦ©¹2Θ§
ΘΫkΘ®xΘΦ0Θ©”–ΝΫΗω≤ΜœύΒ»ΒΡ Β ΐΗυΘ§‘ρkΘΦ©¹2Θ§
Ι ¥πΑΗΈΣkΘΦ©¹2Θ°

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ