题目内容
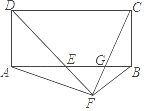
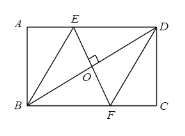
【题目】如图,在矩形ABCD中,AB=3,做BD的垂直平分线E,F,分别与AD、BC交于点E、F,连接BE,DF,若EF=AE+FC,则边BC的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
根据矩形的性质和菱形的性质得∠ABE=∠EBD=∠DBC=30°,AB=BO=3,因为四边形BEDF是菱形,所以可求出BE,AE,进而可求出BC的长.
解:∵四边形ABCD是矩形,
![]()
![]()
![]() 垂直平分
垂直平分![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() 四边形BEDF是菱形,
四边形BEDF是菱形,
∵四边形ABCD是矩形,四边形BEDF是菱形,
∴∠A=90°,AD=BC,DE=BF,OE=OF,EF⊥BD,∠EBO=FBO,
∴AE=FC.又EF=AE+FC,
∴EF=2AE=2CF,
又EF=2OE=2OF,AE=OE,
∴△ABE≌OBE, ∴∠ABE=∠OBE,
∴∠ABE=∠EBD=∠DBC=30°,
∴BE= ![]() =
=![]() ,
,
∴BF=BE=![]() ,
,
∴CF=AE=![]() ,
,
∴BC=BF+CF=![]() ,
,
故选B .

 阳光课堂同步练习系列答案
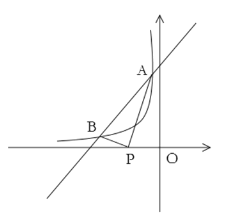
阳光课堂同步练习系列答案【题目】如图,在![]() 中,
中,![]() ,P是
,P是![]() 上的动点,D是
上的动点,D是![]() 延长线上的定点,连接
延长线上的定点,连接![]() 交
交![]() 于点Q.
于点Q.
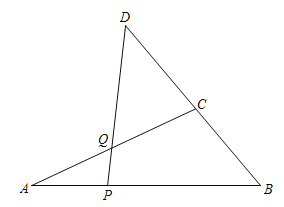
小明根据学习函数的经验,对线段![]() 的长度之间的关系进行了探究.
的长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)对于点P在![]() 上的不同位置,画图测量,得到了线段
上的不同位置,画图测量,得到了线段![]() 的长度(单位:cm)的几组值,如下表:
的长度(单位:cm)的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | |
| 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
| 4.99 | 4.56 | 4.33 | 4.23 | 4.53 | 4.95 | 5.51 |
| 4.99 | 3.95 | 3.31 | 2.95 | 2.80 | 2.79 | 2.86 |
在![]() 的长度这三个量中,确定_________的长度是自变量,_________的长度和_________的长度都是这个自变量的函数;
的长度这三个量中,确定_________的长度是自变量,_________的长度和_________的长度都是这个自变量的函数;
(2)在同一平面直角坐标系![]() 中,画出(1)中所确定的函数的图象;
中,画出(1)中所确定的函数的图象;
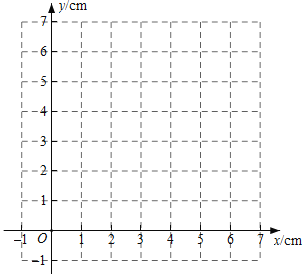
(3)结合函数图象,解决问题:当![]() 时,
时,![]() 的长度约为_______cm.
的长度约为_______cm.
【题目】2020年3月至5月,某校开展了一系列居家阅读活动.学生利用“宅家”时光,在书海中遨游,从阅读中获得精神慰藉和自我提升.为了解学生居家阅读的情况,学校从七、八两个年级各随机抽取50名学生,进行了居家阅读情况调查.下面给出了部分数据信息:
![]() .两个年级学生平均每周阅读时长
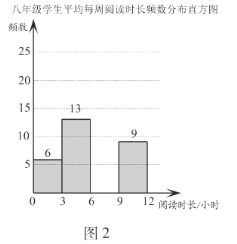
.两个年级学生平均每周阅读时长![]() (单位:小时)的频数分布直方图如下(数据分成4组:
(单位:小时)的频数分布直方图如下(数据分成4组:![]() ,
,![]() ,
,![]() ,
,![]() ):
):

b.七年级学生平均每周阅读时长在![]() 这一组的是:6 6 7 7 7 7 7 8 8 8 8 8 8 8 8 8
这一组的是:6 6 7 7 7 7 7 8 8 8 8 8 8 8 8 8
c.两个年级学生平均每周阅读时长的平均数、中位数、众数、方差如下:
平均数 | 中位数 | 众数 | 方差 | |
七年级 | 6.3 |
| 8 | 7.0 |
八年级 | 6.0 | 7 | 7 | 6.3 |
根据以上信息,回答下列问题:
(1)补全图2;
(2)写出表中![]() 的值;
的值;
(3)返校后,学校计划将平均每周阅读时长不低于9小时的学生授予“阅读之星”称号.小丽说:“根据频数分布直方图中的数据信息,估计七年级约有20%的学生获得该称号,八年级约有18%的学生获得该称号,所以七年级获得该称号的人数一定比八年级获得该称号的人数多.”你认为她的说法________(填入“正确”或“错误”);
(4)请你结合数据对两个年级的居家阅读情况进行评价.
【题目】某租赁公司有![]() 型两种客车,它们的载客量和租金标准如下:
型两种客车,它们的载客量和租金标准如下:
客车类型 | 载客量(人/辆) | 租金(元/辆) |
| 45 | 400 |
| 30 | 280 |
如果某学校计划组织195名师生到培训基地参加社会实践活动,那么租车的总费用最低为____________________元.