Question

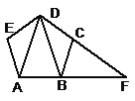
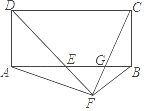
【题目】如图，在矩形ABCD中，∠ADC的平分线与AB交于E，点F在DE的延长线上，∠BFE=90°，连接AF、CF，CF与AB交于G．有以下结论：

①AE=BC

②AF=CF

③BF2=FGFC

④EGAE=BGAB

其中正确的个数是（　　）

A. 1 B. 2 C. 3 D. 4

Answer 1

【答案】C

【解析】

①只要证明△ADE为等腰直角三角形即可

②只要证明△AEF≌△CBF（SAS）即可；

③假设BF2=FGFC，则△FBG∽△FCB，推出∠FBG=∠FCB=45°，由∠ACF=45°，推出∠ACB=90°，显然不可能，故③错误，

④由△ADF∽△GBF，可得，由EG∥CD，推出，推出，由AD=AE，EGAE=BGAB，故④正确，

①DE平分∠ADC，∠ADC为直角，

∴∠ADE=×90°=45°，

∴△ADE为等腰直角三角形，

∴AD=AE，

又∵四边形ABCD矩形，

∴AD=BC，

∴AE=BC

②∵∠BFE=90°，∠BFE=∠AED=45°，

∴△BFE为等腰直角三角形，

∴则有EF=BF

又∵∠AEF=∠DFB+∠ABF=135°，∠CBF=∠ABC+∠ABF=135°，

∴∠AEF=∠CBF

在△AEF和△CBF中，AE=BC，∠AEF=∠CBF，EF=BF，

∴△AEF≌△CBF（SAS）

∴AF=CF

③假设BF2=FGFC，则△FBG∽△FCB，

∴∠FBG=∠FCB=45°，

∵∠ACF=45°，

∴∠ACB=90°，显然不可能，故③错误，

④∵∠BGF=180°-∠CGB，∠DAF=90°+∠EAF=90°+（90°-∠AGF）=180°-∠AGF，∠AGF=∠BGC，

∴∠DAF=∠BGF，∵∠ADF=∠FBG=45°，

∴△ADF∽△GBF，

∴，

∵EG∥CD，

∴，

∴，∵AD=AE，

∴EGAE=BGAB，故④正确，

故选C．