Question

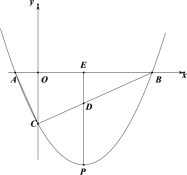
【题目】如图，平面直角坐标系，抛物线（，）与轴交于A、B两点（A在B左侧），与轴交于点C，过抛物线的顶点P且与轴平行的直线交BC于点D，且满足BD：CD=3：2，

（1）若∠ACB=90°，求抛物线解析式；

（2）问OC和DP能否相等？若能，求出抛物线解析式，若不能，说明理由．

Answer 1

【答案】（1）；（2）不能，理由见解析

【解析】

（1）根据平行线分线段成比例定理结合对称轴的性质得到，BE=AE，设BE=AE=3m，则OE=2m，AO=m，再证得△AOC∽△COB，根据对应边成比例，列式可求得的值，即求得点A、B的坐标，利用待定系数法即可求解；

（2）由（1）知：A（-m，0），B（5m，0），可求得抛物线的解析式为，则顶点为P（2m，-9），即EP=9，根据△BDE∽△BCO求得DE的长，DP的长，从而证明OC和DP不可能相等．

（1）设直线交x轴于点E，

∵直线∥轴，即DE∥OC，

∴，

∵直线经过顶点P，

∴直线是抛物线的对称轴，

∴BE=AE，

设BE=AE=3m，则OE=2m，AO=m，

当∠ACB=90°时，

∵∠ACO+∠BCO=90，∠ACO+∠CAO=90，

∴∠CAO=∠BCO，

∴△AOC∽△COB，

∴，

故OC=AO·BO，即5=m·5m，

解得或(舍去)，

∴A（，0），B（，0），

将A，B坐标代入，

得：，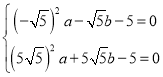

解得，

故二次函数的解析式为；

（2）由（1）知：A（-m，0），B（5m，0），

设二次函数的解析式为，

将C（0，-5）代入得：，

解得，

∴，

故P（2m，-9），即EP=9，

∵DE∥OC，

∴△BDE∽△BCO，

∴，且OC=5，

∵BD:CD=3:2，

∴DE=，

∴PD=9-3=6，

∵5≠6，

∴OC≠DP，

故OC和DP不可能相等．