题目内容
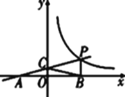
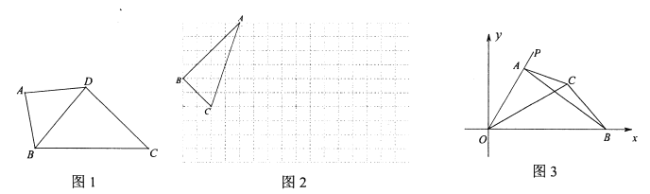
【题目】如图,已知AB是⊙O的直径,P是BA延长线上一点,PC切⊙O于点C,CD⊥AB,垂足为D.
(1)求证:∠PCA=∠ABC;
(2)过点A作AE∥PC交⊙O于点E,交CD于点F,交BC于点M,若∠CAB=2∠B,CF=![]() ,求阴影部分的面积.
,求阴影部分的面积.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)如图,连接OC,利用圆的切线的性质和直径对应的圆周角是直角可得∠PCA=∠OCB,利用等量代换可得∠PCA=∠ABC.
(2)先求出△OCA是等边三角形,在利用三角形的等边对等角定理求出FA=FC和CF=FM,然后分别求出AM、AC、MO、CD的值,分别求出![]() 、
、![]() 、
、![]() 的值,利用
的值,利用![]() ,然后通过计算即可解答.
,然后通过计算即可解答.
解:(1)证明:连接OC,如图,
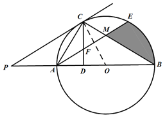
∵PC切⊙O于点C,∴OC⊥PC,
∴∠PCA+∠ACO=90,
∵AB是⊙O的直径,∴∠ACB=∠ACO+OCB=90
∴∠PCA=∠OCB,
∵OC=OB,∴∠OBC=∠OCB,
∴∠PCA=∠ABC;
(2)连接OE,如图,
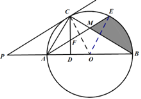
∵△ACB中,∠ACB=90,∠CAB=2∠B,
∴∠B=30,∠CAB=60,∴△OCA是等边三角形,
∵CD⊥AB,∴∠ACD+∠CAD=∠CAD+∠ABC=90,
∴∠ACD=∠B=30,
∵PC∥AE,∴∠PCA=∠CAE=30,∴FC=FA,
同理,CF=FM,∴AM=2CF=![]() ,
,
Rt△ACM中,易得AC=![]() ×
×![]() =3=OC,
=3=OC,
∵∠B=∠CAE=30,∴∠AOC=∠COE=60,
∴∠EOB=60,∴∠EAB=∠ABC=30,∴MA=MB,
连接OM,EG⊥AB交AB于G点,如图所示,
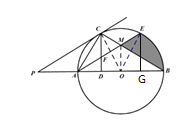
∵OA=OB,∴MO⊥AB,∴MO=OA×tan30=![]() ,
,
∵△CDO≌△EDO(AAS),
∴EG=CD=AC×sin60=![]() ,
,
∴![]() ,
,
同样,易求![]() ,
,
![]()
∴![]() =
=![]() .
.

 名校课堂系列答案
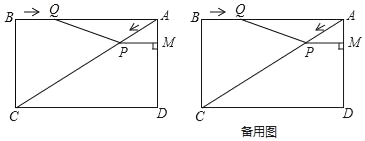
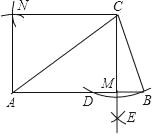
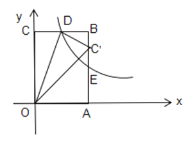
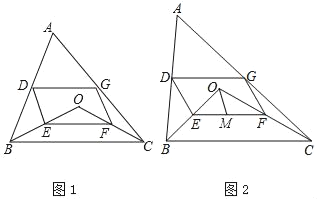
名校课堂系列答案【题目】如图1,点D、E、F、G分别为线段AB、OB、OC、AC的中点.
(1)求证:四边形DEFG是平行四边形;
(2)如图2,若点M为EF的中点,BE:CF:DG=2:3:![]() ,求证:∠MOF=∠EFO.
,求证:∠MOF=∠EFO.
【题目】为迎接中国森博会,某商家计划从厂家采购A,B两种产品共20件,产品的采购单价(元/件)是采购数量(件)的一次函数,下表提供了部分采购数据.
采购数量(件) | 1 | 2 | … |
A产品单价(元/件) | 1480 | 1460 | … |
B产品单价(元/件) | 1290 | 1280 | … |
(1)设A产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的![]() ,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完,在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润.