题目内容
【题目】为迎接中国森博会，某商家计划从厂家采购A，B两种产品共20件，产品的采购单价（元/件）是采购数量（件）的一次函数，下表提供了部分采购数据．
采购数量（件） | 1 | 2 | … |
A产品单价（元/件） | 1480 | 1460 | … |
B产品单价（元/件） | 1290 | 1280 | … |
（1）设A产品的采购数量为x（件），采购单价为y1（元/件），求y1与x的关系式；
（2）经商家与厂家协商，采购A产品的数量不少于B产品数量的
，且A产品采购单价不低于1200元，求该商家共有几种进货方案；
（3）该商家分别以1760元/件和1700元/件的销售单价售出A，B两种产品，且全部售完，在（2）的条件下，求采购A种产品多少件时总利润最大，并求最大利润．
【答案】(1)y1=﹣20x+1500（0＜x≤20，x为整数）；(2)商家共有5种进货方案；（3）当x=15时，W最大=10650.
【解析】试题分析：（1）首先设出函数解析式，然后根据表格将数字代入进行求解；（2）根据题意列出关于x的不等式组，然后根据x为整数，求出x的值；（3）设总利润为w，列出w和x的二次函数关系式，然后根据二次函数的增减性进行求解.
试题解析：（1）设y1与x的关系式y1=kx+b，由表知
，
解得k=﹣20，b=1500， 即y1=﹣20x+1500（0＜x≤20，x为整数），
（2）根据题意可得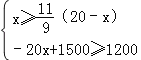
， 解得11≤x≤15， ∵x为整数，
∴x可取的值为：11，12，13，14，15， ∴该商家共有5种进货方案；
（3）令总利润为W，则W=30x2﹣540x+1200=30（x﹣9）2+9570，
∵a=30＞0， ∴当x≥9时，W随x的增大而增大， ∵11≤x≤15，
∴当x=15时，W最大=10650；
练习册系列答案
相关题目
