题目内容
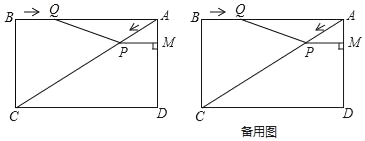
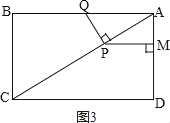
【题目】已知:如图,在矩形ABCD中,AC是对角线,AB=8cm,BC=6cm.点P从点A出发,沿AC方向匀速运动,速度为2cm/s,同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s.过点P作PM⊥AD于点M,连接PQ,设运动时间为t(s)(0<t<4),解答下列问题:
(1)当t为何值时,点Q在线段AC的中垂线上;
(2)写出四边形PQAM的面积为S(cm2)与时间t的函数关系式;
(3)是否存在某一时刻t,使S四边形PQAM:S矩形ABCD=9:50?若存在,求出t的值;若不存在,请说明理由;
(4)当t为何值时,△APQ与△ADC相似.
【答案】(1)t=![]() ;(2)S四边形PQAM=﹣
;(2)S四边形PQAM=﹣![]() t2+
t2+![]() t;(3)存在t=2,使S四边形PQAM=
t;(3)存在t=2,使S四边形PQAM=![]() S矩形ABCD;(4)当t=
S矩形ABCD;(4)当t=![]() 或
或![]() 时,△APQ与△ABC相似.
时,△APQ与△ABC相似.
【解析】试题分析:(1)由点Q在线段AC的中垂线上可知CQ=AQ=8﹣2t,在Rt△BCQ中根据BC2+BQ2=CQ2列方程求解.
(2)先证明△APM∽△ACD,列方程用含t的代数式表示出AM和PM的值,然后根据四边形PQAM的面积=△APQ的面积+△APM的面积求解;
(3)存在t=2,使S四边形PQAM=![]() S矩形ABCD.首先根据四边形ABCD是矩形,求出S矩形ABCD的值是多少;然后分别求出△APM、△APQ的面积各是多少,再根据S四边形PQAM=
S矩形ABCD.首先根据四边形ABCD是矩形,求出S矩形ABCD的值是多少;然后分别求出△APM、△APQ的面积各是多少,再根据S四边形PQAM=![]() S矩形ABCD,求出t的值是多少即可.
S矩形ABCD,求出t的值是多少即可.
(4)当t=2![]() 或1
或1![]() 时,△APQ与△ABC相似.根据题意,分两种情况讨论:①当∠AQP=90°时,△APQ与△ABC相似;②当∠APQ=90°时,△APQ与△ABC相似;求出当t为何值时,△APQ与△ABC相似即可.
时,△APQ与△ABC相似.根据题意,分两种情况讨论:①当∠AQP=90°时,△APQ与△ABC相似;②当∠APQ=90°时,△APQ与△ABC相似;求出当t为何值时,△APQ与△ABC相似即可.
解:(1)由题意CQ=AQ=8﹣2t,
在Rt△BCQ中,∵BC2+BQ2=CQ2,
∴62+(2t)2=(8﹣2t)2,
解得t=![]() .
.
(2)∵四边形ABCD是矩形,
∴S矩形ABCD=ABBC=8×6=48,
∵PM⊥AD,CD⊥AD,
∴PM∥CD,
∴△APM∽△ACD,
∴![]() =
=![]() =
=![]() ,
,
即 ![]() =
=![]() =
=![]() ,
,
解得AM=![]() t,PM=
t,PM=![]() t,
t,
∴S△APM=![]() AMPM=
AMPM=![]() ×
×![]() t×
t×![]() t=
t=![]() t2.
t2.
∵sin∠PAQ=![]() =
=![]() ,
,
∴S△APQ=![]() APAQsin∠PAQ=
APAQsin∠PAQ=![]() ×2t(8﹣2t)×
×2t(8﹣2t)×![]() =
=![]() t(4﹣t),
t(4﹣t),
∵S四边形PQAM=![]() t2+
t2+![]() t(4﹣t)=﹣
t(4﹣t)=﹣![]() t2+
t2+![]() t.
t.
(3)存在t=2,使S四边形PQAM=![]() S矩形ABCD.
S矩形ABCD.
如图2,
 ,
,
∵S四边形PQAM=![]() S矩形ABCD,
S矩形ABCD,
∴![]() t2+
t2+![]() t(4﹣t)=
t(4﹣t)=![]() ×48,
×48,
整理,可得t2﹣20t+36=0
解得t=2或t=18(舍去),
∴存在t=2,使S四边形PQAM=![]() S矩形ABCD.
S矩形ABCD.
(4)当t=2![]() 或1
或1![]() 时,△APQ与△ABC相似.
时,△APQ与△ABC相似.
①当△APQ∽△ACB,
∴![]() =
=![]() ,
,
即 ![]() =
=![]() ,
,
解得t=2![]() ,
,
②如图3,
 ,
,
当∠APQ=90°时,△APQ与△ABC相似,
∵tan∠PAQ=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
即 ![]() =
=![]() ,
,
∴PQ=![]() t,
t,
∵BQ=t,
∴AQ=8﹣2t,
在Rt△APQ中,
∵AP2+PQ2=AQ2,
∴(2t)2+(![]() t)2=(8﹣2t)2,
t)2=(8﹣2t)2,
解得t=1![]() 或t=﹣16(舍去).
或t=﹣16(舍去).
综上,可得
当t=2![]() 或1
或1![]() 时,△APQ与△ABC相似.
时,△APQ与△ABC相似.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案【题目】嘉兴某校组织了“垃圾分类”知识竞赛活动,获奖同学在竞赛中的成绩绘成如下图表,
根据图表提供的信息解答下列问题:
垃圾分类知识竞赛活动成绩统计表
分数段 | 频数 | 频数频率 |
80≤x<85 | x | 0.2 |
85≤x<90 | 80 | y |
90≤x<95 | 60 | 0.3 |
95≤x<100 | 20 | 0.1 |
(1)求本次获奖同学的人数;
(2)求表中x,y的数值:并补全频数分布直方图.

【题目】某林场要考察一种幼树在一定条件下的移植成活率,在移植过程中的统计结果如下表所示:
移植的幼树n/棵 | 500 | 1000 | 2000 | 4000 | 7000 | 10000 | 12000 | 15000 |
成活的幼树m/棵 | 423 | 868 | 1714 | 3456 | 6020 | 8580 | 10308 | 12915 |
成活的频率 | 0.846 | 0.868 | 0.857 | 0.864 | 0.860 | 0.858 | 0.859 | 0.861 |
在此条件下,估计该种幼树移植成活的概率为_________________(精确到![]() );若该林场欲使成活的幼树达到4.3万棵,则估计需要移植该种幼树_________万棵.
);若该林场欲使成活的幼树达到4.3万棵,则估计需要移植该种幼树_________万棵.