Question

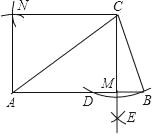
【题目】如图，已知等腰△ABC中，AB＝AC．以C为圆心，CB的长为半径作弧，交AB于点D．分别以B、D为圆心，大于BD的长为半径作弧，两弧交于点E．作射线CE交AB于点M．分别以A、C为圆心，CM、AM的长为半径作弧，两弧交于点N．连接AN、CN

（1）求证：AN⊥CN

（2）若AB＝5，tanB＝3，求四边形AMCN的面积．

Answer 1

【答案】（1）详见解析；（2）12.

【解析】

(1)由作图可知四边形AMCN是平行四边形，CM⊥AB，据此即可得答案；

(2)在Rt△CBM中，利用tan∠B＝＝3，由此可以设BM＝k，CM＝3k，表示出AM，然后在Rt△ACM中，利用勾股定理求出k的值，继而求得CM＝3，AM＝4，利用矩形面积公式即可求得答案.

(1)由作图可知：CN＝AM，AN＝CM，

∴四边形AMCN是平行四边形，

∵CM⊥AB，

∴∠AMC＝90°，

∴四边形AMCN是矩形，

∴∠ANC＝90°，

∴AN⊥CN．

(2)在Rt△CBM中，∵tan∠B＝＝3，

∴可以假设BM＝k，CM＝3k，

∵AC＝AB＝5，

∴AM＝5﹣k，

在Rt△ACM中，∵AC2＝CM2+AM2，

∴25＝(3k)2+(5﹣k)2，

解得k＝1或0(舍弃)，

∴CM＝3，AM＝4，

∴四边形AMCN的面积＝CMAM＝12．