题目内容
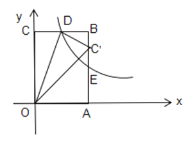
【题目】如图,平面直角坐标系中,矩形ABCD与双曲线![]() 交于D、E两点,将△OCD沿OD翻折,点C的对称C'恰好落在边AB上,已知OA=3,OC=5,则AE长为()
交于D、E两点,将△OCD沿OD翻折,点C的对称C'恰好落在边AB上,已知OA=3,OC=5,则AE长为()
A. 4B. ![]() C.
C. ![]() D. 3
D. 3
【答案】B
【解析】
由翻折的性质可知OC′=5,由勾股定理可求得AC′=4,故此可知BC′=1,设CD=x,由翻折的性质可知DC′=x,则DB=3-x,依据勾股定理可求得CD的长,从而得到点D的坐标,于是可求得双曲线的解析式,最后将x=3代入解析式求得点E的坐标,从而可知AE的长.
设CD=x.
由翻折的性质可知;OC′=OC=5,CD=DC′=x,则BD=3-x.
∵在Rt△OAC′中,AC′=![]() =4.
=4.
∴BC′=1.
在Rt△DBC′,由勾股定理可知:DC′2=DB2+BC′2,即x2=(3-x)2+12.
解得:x=![]() .
.
∴k=CDOC=![]() ×5=
×5=![]() .
.
∴双曲线的解析式为y=![]() .
.
将x=3代入得:y=![]() .
.
∴AE=![]() .
.
故选B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目