题目内容
【题目】四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似但不全等,我们就把这条对角线叫做这个四边形的“相似对角线”.
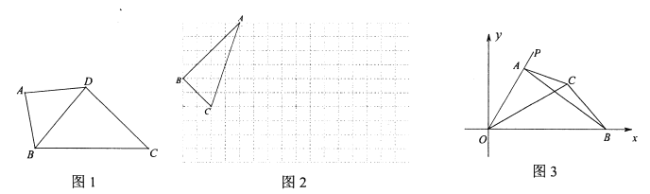
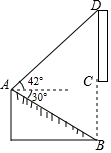
(1)如图1,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,对角线
,对角线![]() 平分
平分![]() .求证:
.求证:![]() 是四边形
是四边形![]() 的“相似对角线”;
的“相似对角线”;
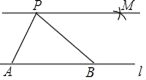
(2)如图2,已知格点![]() ,请你在正方形网格中画出所有的格点四边形
,请你在正方形网格中画出所有的格点四边形![]() ,使四边形
,使四边形![]() 是以
是以![]() 为“相似对角线”的四边形;(注:顶点在小正方形顶点处的多边形称为格点多边形)
为“相似对角线”的四边形;(注:顶点在小正方形顶点处的多边形称为格点多边形)
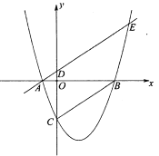
(3)如图3,四边形![]() 中,点
中,点![]() 在射线
在射线![]() :
:![]() 上,点
上,点![]() 在
在![]() 轴正半轴上,对角线
轴正半轴上,对角线![]() 平分
平分![]() ,连接
,连接![]() .若
.若![]() 是四边形
是四边形![]() 的“相似对角线”,
的“相似对角线”,![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)证明见解析;(2)见解析;(3)![]() .
.
【解析】
(1)由BD平分∠ABC可得∠ABD=∠DBC=50,则∠BDC+∠A=130°,根据∠ADC=130°可得∠ADB=∠C,即可求解;
(2)如图所示,根据两个三角形夹角相等,夹边成比例,则三角形相似,即可求解;
(3)利用△AOC∽△COB,则OAOB=OC2,而S△AOB=![]() ×OB×yA=
×OB×yA=![]() ×OB×OAsin60°=6
×OB×OAsin60°=6![]() ,即可求解.
,即可求解.
解:(1)∵对角线![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是四边形
是四边形![]() 的“相似对角线”;
的“相似对角线”;
(2)如下图所示:
∵∠ABC=∠ACD1=90°,
![]() ,
,
∴△ABC∽△ACD1,
故:以AC为“相似对角线”的四边形有:ABCD1,
同理可得:以AC为“相似对角线”的四边形还有:ABCD2、ABCD3、ABCD4;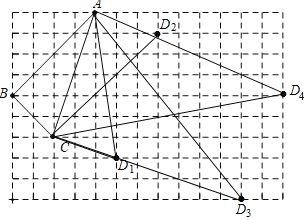
(3)如图,作![]() 于
于![]() ,
,![]() 于
于![]() ,
,
∵点![]()
![]() :
:![]() 上,
上,
∴![]() ,即
,即![]() ,
,
∵对角线![]() 平分
平分![]() ,
,
∴![]() ,
,
∵![]() 是四边形
是四边形![]() 的“相似对角线”,
的“相似对角线”,
∴![]() 与
与![]() 相似且不全等,
相似且不全等,
∴![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
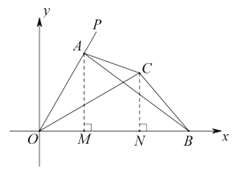
故答案为:(1)证明见解析;(2)见解析;(3)![]() .
.

【题目】华联超市用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该商场购进甲、乙两种商品各多少件?
(2)该超市将购进的甲、乙两种商品全部卖完后一共可获得多少利润?