题目内容
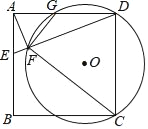
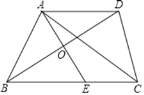
【题目】如图1,点D、E、F、G分别为线段AB、OB、OC、AC的中点.
(1)求证:四边形DEFG是平行四边形;
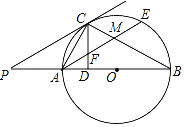
(2)如图2,若点M为EF的中点,BE:CF:DG=2:3:![]() ,求证:∠MOF=∠EFO.
,求证:∠MOF=∠EFO.
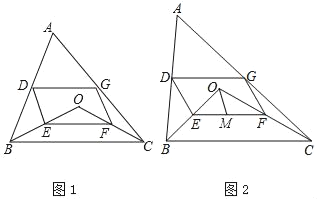
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)根据中位线定理得:DG∥BC,![]() ,则DG=BC,DE∥BC,根据一组对边平行且相等的四边形是平行四边形可得:四边形DEFG是平行四边形;
,则DG=BC,DE∥BC,根据一组对边平行且相等的四边形是平行四边形可得:四边形DEFG是平行四边形;
(2)先根据已知的比的关系设未知数:设BE=2x,CF=3x,![]() ,根据勾股定理的逆定理得:∠EOF=90°,最后利用直角三角形斜边中线的性质可得OM=FM,由等边对等角可得结论.
,根据勾股定理的逆定理得:∠EOF=90°,最后利用直角三角形斜边中线的性质可得OM=FM,由等边对等角可得结论.
解:(1)∵D是AB的中点,G是AC的中点,
∴DG是△ABC的中位线,
∴DG∥BC,DG=![]() BC,
BC,
同理得:EF是△OBC的中位线,
∴EF∥BC,EF=![]() BC,
BC,
∴DG=EF,DG∥EF,
∴四边形DEFG是平行四边形;
(2)∵BE:CF:DG=2:3:![]() ,
,
∴设BE=2x,CF=3x,DG=![]() ,
,
∴OE=2x,OF=3x,
∵四边形DEFG是平行四边形,
∴DG=EF=![]() ,
,
∴OE2+OF2=EF2,
∴∠EOF=90°,
∵点M为EF的中点,
∴OM=MF,
∴∠MOF=∠EFO.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案【题目】某校九年级八个班共有280名学生,男女生人数大致相同,调查小组为调查学生的体质健康水平,开展了一次调查研究,请将下面的过程补全.
收集数据:
(1)调查小组计划选取40名学生的体质健康测试成绩作为样本,下面的取样方法中,合理的是___________(填字母);
A.抽取九年级1班、2班各20名学生的体质健康测试成绩组成样本
B.抽取各班体育成绩较好的学生共40名学生的体质健康测试成绩组成样本
C.从年级中按学号随机选取男女生各20名学生学生的体质健康测试成绩组成样本
整理、描述数据:
抽样方法确定后,调查小组获得了40名学生的体质健康测试成绩如下:
77 83 80 64 86 90 75 92 83 81
85 86 88 62 65 86 97 96 82 73
86 84 89 86 92 73 57 77 87 82
91 81 86 71 53 72 90 76 68 78
整理数据,如下表所示:
2018年九年级部分学生学生的体质健康测试成绩统计表
|
|
|
|
|
|
|
|
|
|
1 | 1 | 2 | 2 | 4 | 5 | 5 | 2 |
分析数据、得出结论
调查小组将统计后的数据与去年同期九年级的学生的体质健康测试成绩(直方图)进行了对比,
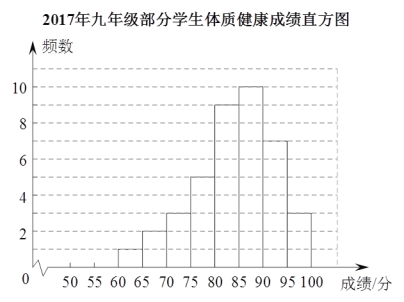
(2)你能从中得到的结论是_____________,你的理由是________________________________.
(3)体育老师计划根据2018年的统计数据安排75分以下的同学参加体质加强训练项目,则全年级约有________名同学参加此项目.