题目内容
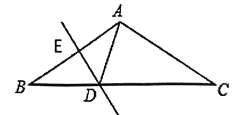
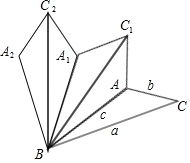
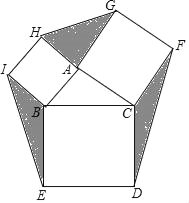
【题目】如图,△ABC中,AB=2,AC=3,1<BC<5,分别以AB、BC、AC为边向外作正方形ABIH、BCDE和正方形ACFG,则图中阴影部分的最大面积为( )
A. 6 B. 9 C. 11 D. 无法计算
【答案】B
【解析】
有旋转的性质得到CB=BE=BH′,推出C、B、H'在一直线上,且AB为△ACH'的中线,得到S△BEI=S△ABH′=S△ABC,同理:S△CDF=S△ABC,当∠BAC=90°时, S△ABC的面积最大,S△BEI=S△CDF=S△ABC最大,推出S△GBI=S△ABC,于是得到阴影部分面积之和为S△ABC的3倍,于是得到结论.
把△IBE绕B顺时针旋转90°,使BI与AB重合,E旋转到H'的位置,
∵四边形BCDE为正方形,∠CBE=90°,CB=BE=BH′,
∴C、B、H'在一直线上,且AB为△ACH'的中线,
∴S△BEI=S△ABH′=S△ABC,
同理:S△CDF=S△ABC,
当∠BAC=90°时,
S△ABC的面积最大,
S△BEI=S△CDF=S△ABC最大,
∵∠ABC=∠CBG=∠ABI=90°,
∴∠GBE=90°,
∴S△GBI=S△ABC,
所以阴影部分面积之和为S△ABC的3倍,
又∵AB=2,AC=3,
∴图中阴影部分的最大面积为3×![]() ×2×3=9,
×2×3=9,
故选:B.

练习册系列答案
相关题目