题目内容
【题目】已知在平面直角坐标系中有三点
、
、
.请回答如下问题：
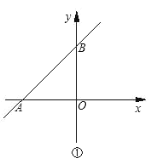
（1）在坐标系内描出
；
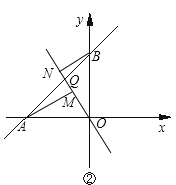
（2）在坐标系中画出
，使它与关于
轴对称；
（3）在
轴上找一点
，使
的值最小，并求出此最小值.
【答案】（1）见解析；（2）见解析；（3）作图见解析，
的值最小值为
.
【解析】
（1）在坐标系内描出各点，顺次连接各点即可；
（2）分别作出各顶点关于x轴的对称点，再顺次连接即可；
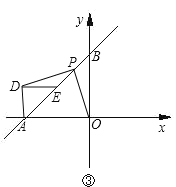
（3）作点C关于y轴的对称点D，连接BD，则BD交y轴即为点P，则此时PB+PC的值最小，而且其最小值为线段BD的长，再根据勾股定理求出结果．
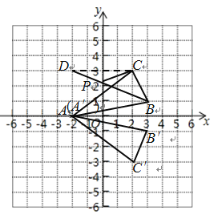
解：（1）（2）如图所示；
（3）如图，作点C关于y轴的对称点D，连接BD，则BD交y轴即为点P，则此时PB+PC的值最小.
根据对称性可知，CP=DP，
∴PB+PC=BP+DP=BD=
.
即的最小值为.
练习册系列答案
相关题目
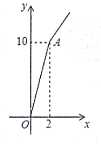
【题目】某玉米种子的价格为
元/千克，如果一次购买2千克以上的种子，超过2千克部分的种子价格打8折，某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析，并绘制出了函数图象，以下是该科技人员绘制的图象和表格的不完整资料，已知点A的坐标为
，请你结合表格和图象：
付款金额 |
| 7.5 | 10 | 12 |
|
购买量 | 1 | 1.5 | 2 | 2.5 | 3 |
（1）
，
；
（2）求出当
时，
关于
的函数解析式；
