题目内容
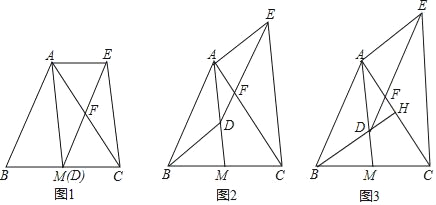
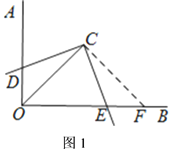
【题目】(1)如图1,已知![]() 中,
中,![]() ,
,![]() ,垂足为
,垂足为![]() ,
,![]() ,则
,则![]() ___
___![]() .
.
(2)若把(1)中![]() 改为
改为![]() ,其它条件不变,请用含
,其它条件不变,请用含![]() 的式子表示
的式子表示![]() ,并证明 你的结论.
,并证明 你的结论.
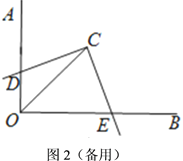
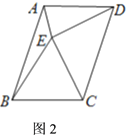
(3)如图2,四边形![]() 中,
中,![]() ,点
,点![]() 在四边形
在四边形![]() 内部,在
内部,在![]() 中,
中,![]() ,且
,且![]() ,连接
,连接![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
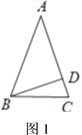
【答案】(1)20°;(2)![]() ;(3)∠AEB=135°.
;(3)∠AEB=135°.
【解析】
(1)在△ABC中利用等腰三角形性质与三角形内角和得到∠C=70°,再利用直角三角形性质在直角三角形BCD中,即可得到∠DBC;(2)在△ABC中利用等腰三角形性质与三角形内角和得到![]() ,再利用直角三角形性质在直角三角形BCD中,即可得到
,再利用直角三角形性质在直角三角形BCD中,即可得到![]() ;(3)过点
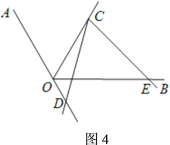
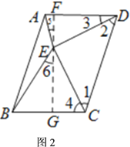
;(3)过点![]() 作
作![]() 于
于![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,在△DEC、△ADE、△BCE中利用三角形内角和定理,列出关系式,利用等量代换关系即可求解.
,在△DEC、△ADE、△BCE中利用三角形内角和定理,列出关系式,利用等量代换关系即可求解.
(1)∵ ![]() ,
,![]()
∴∠C=![]() =70°
=70°
又∵![]()
∴∠BDC=90°
∴∠DBC=90°-70°=20°
(2)![]()
证明:![]() ,
,
![]() ,
,
![]()
![]() 在
在![]() 中,
中,
![]() .
.
(3)过点![]() 作
作![]() 于
于![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,
,
则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
由(2)得![]() ,
,
![]() ,
,
![]() .
.

练习册系列答案
相关题目