Question

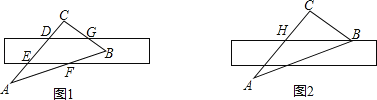
【题目】如图①，将直尺摆放在三角板上，使直尺与三角板的边分别交于点D、E、F、G，∠CGD＝42°，将直尺向下平移，使直尺的边缘通过点B，交AC于点H，如图②所示．

（1）∠CBH的大小为　 　度．

（2）点H、B的读数分别为4、13.4，求BC的长．（结果精确到0.01）

（参考数据：sin42°＝0.67，cos42°＝0.74，tan42°＝0.90）

Answer 1

【答案】（1）42°；（2）BC的长约为6.96．

【解析】

（1）利用平行线的性质求解；

（2）先计算出BH，然后根据余弦的定义求BC的长．

（1）根据平移的性质

∴∠CBH＝42°；

故答案为：42°；

（2）由图得，BH＝13.4﹣4＝9.4，

在Rt△BCH中，∠C＝90°，∠CBH＝42°，

∵cos∠CBH＝，

∴BC＝9.4×cos42°＝9.4×0.74≈6.96．

即BC的长约为6.96．