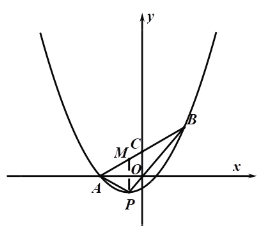
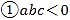题目内容
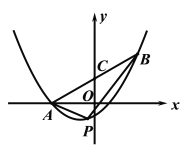
【题目】如图,抛物线![]() 过点
过点![]() 和点
和点![]() ,连结AB交y轴于点C.
,连结AB交y轴于点C.
(1)求抛物线的函数解析式;
(2)点P在线段AB下方的抛物线上运动,连结AP,BP. 设点P的横坐标为m,△ABP的面积为s.
①求s与m的函数关系式;
②当s取最大值时,抛物线上是否存在点Q,使得S△ACQ=s. 若存在,求点Q的坐标;若不存在,说明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②Q点坐标为
;②Q点坐标为![]() 或
或![]() .
.
【解析】
(1)直接把A、B代入解析式求解即可;
(2)①根据自变量与函数值的对应关系,可得P点坐标,M点坐标,根据线段的和差,可得PM的长,A到PM的距离,B到PM的距离,根据三角形的面积公式,可得答案;
②由①得到点P坐标,根据S△ACQ=s,得到直线AB向上平移3个单位的直线,联立![]() 和
和![]() 即可得解.
即可得解.
(1)把点![]() 和点
和点![]() 代入
代入![]() 得:
得:
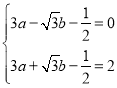 ,.
,.
解得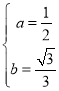 .
.
∴![]() ..
..
(2)∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,![]() .
.
∴![]()
∴![]() ,即
,即![]() .
.
当![]() 时,最大值
时,最大值![]() .
.
(2)当△ABP的面积取最大值时,P点坐标为![]() .
.
∴![]() .
.
∵S△ACQ=S△ABP,∴S△AQB=2S△ABP,
∴可使直线AB向上平移3个单位长度,得![]()
联立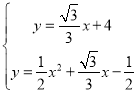 ,解得Q点坐标为
,解得Q点坐标为![]() 或
或![]() .
.

练习册系列答案
相关题目