Question

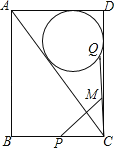
【题目】如图，矩形ABCD，AD＝6，AB＝8，点P为BC边上的中点，点Q是△ACD的内切圆圆O上的一个动点，点M是CQ的中点，则PM的最大值是（　　）

A.﹣1B.+1C.3.2D.3

Answer 1

【答案】B

【解析】

由矩形的性质得出∠D＝90°，CD＝AB＝8，由勾股定理得出AC＝＝10，设△AD的内切圆O的半径为r，则×10r+×8r+×6r＝×8×6，解得r＝2，连接BQ，易证PM是△BCQ的中位线，得出PM＝BQ，当BQ经过圆心O时，BQ最长，则此时PM最长，作OE⊥AD于E，OF⊥AB于F，则BF＝AB﹣AF＝6，OF＝AE＝AD﹣DE＝4，由勾股定理得出BO＝，则BQ＝BO+OQ＝，即可得出结果．

∵四边形ABCD是矩形，

∴∠D＝90°，CD＝AB＝8，

∴AC＝＝＝10，

设△AD的内切圆O的半径为r，

则×10r+×8r+×6r＝×8×6，

解得：r＝2，

连接BQ，

∵P是BC边上的中点，点M是CQ的中点，

∴PM是△BCQ的中位线，

∴PM＝BQ，

当BQ经过圆心O时，BQ最长，则此时PM最长，

作OE⊥AD于E，OF⊥AB于F，

则BF＝AB﹣AF＝8﹣2＝6，OF＝AE＝AD﹣DE＝6﹣2＝4，

∴BO＝，

∴BQ＝BO+OQ＝

∴PM＝BQ＝.

故选：B．