Question

【题目】已知，在△PAB中，PA＝PB，经过A、B作⊙O．

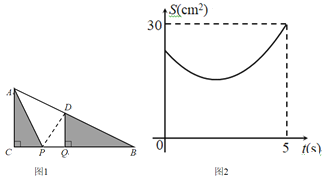
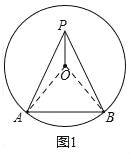
（1）如图1，连接PO，求证：PO平分∠APB；

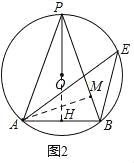
（2）如图2，点P在⊙O上，PA：AB＝：2，E是⊙O上一点，连接AE、BE．求tan∠AEB的值；

（3）如图3，在（2）的条件下，AE经过圆心O，AE交PB于点F，过F作FG⊥BE于点G，EF+BG＝14，求线段OF的长度．

Answer 1

【答案】（1）见解析；（2）；（3）

【解析】

(1) 连接OA，OB，证明OP是AB的垂直平分线即可;

(2) 延长PO，交AB于H，过点A作AM⊥PB于M，由PH垂直平分AB和 PA：AB＝：2，设AB＝2，则AP＝BP＝，AH＝BH＝1，然后根据勾股定理和锐角的三角函数进行解答即可;

(3) 连接PO并延长，交AB于点H，由PH垂直平分AB，可得AE为直径，设设FG＝3x，则EG＝4x，EF＝5x，再运用勾股定理和相似三角形知识进行解答即可.

（1）证明：连接OA，OB，

则OA＝OB，

又∵PA＝PB，

∴PO垂直平分AB，

∴PO平分∠APB；

（2）解：延长PO，交AB于H，过点A作AM⊥PB于M，

由（1）知PH垂直平分AB，

∵PA：AB＝：2，

∴设AB＝2，则AP＝BP＝，AH＝BH＝1，

∴在Rt△PAH中，

PH＝ ＝3，

∵S△PAB＝ABPH＝PBAM，

∴2×3＝×AM，

∴AM＝，

在Rt△PAM中，

PM＝＝，

∴tan∠APM＝＝：＝=，

∵∠AEB＝∠APM，

∴tan∠AEB＝；

（3）连接PO并延长，交AB于点H，由（1）知，PH垂直平分AB，

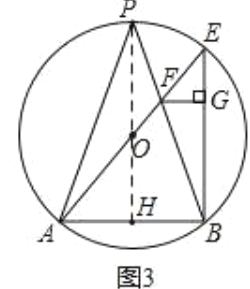
∵AE为直径，在Rt△EFG中，tan∠FEG＝，

∴设FG＝3x，则EG＝4x，EF＝5x，

∵EF+BG＝14，

∴BG＝14﹣5x，

∴∠ABE＝90°＝∠AHP＝∠PHB，

∴PH∥EB，

∴∠HPB＝∠GBF，

∴△HPB∽△GBF，

∴，

∴，

解得，x＝1，

∴EF＝5，BE＝BG+EG＝9+4＝13，

∴AB＝BE＝，

∴AE＝ ，

∴OE＝AE＝，

∴OF＝OE﹣EF＝﹣5＝，

∴线段OF的长度为．