题目内容
【题目】在初中阶段的函数学习中我们经历了“确定函数的表达,利用函数图象研究其性质﹣﹣运用函数解决问题”的学习过程,在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.已知函数y=2![]() ﹣b的定义域为x≥﹣3,且当x=0时y=2
﹣b的定义域为x≥﹣3,且当x=0时y=2![]() ﹣2由此,请根据学习函数的经验,对函数y=2
﹣2由此,请根据学习函数的经验,对函数y=2![]() ﹣b的图象与性质进行如下探究:
﹣b的图象与性质进行如下探究:
(1)函数的解析式为: ;
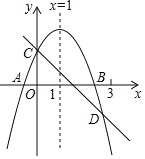
(2)在给定的平面直角坐标系xOy中,画出该函数的图象并写出该函数的一条性质: ;
(3)结合你所画的函数图象与y=x+1的图象,直接写出不等式2![]() ﹣b≤x+1的解集.
﹣b≤x+1的解集.
【答案】(1)y=2![]() ﹣2;(2)当x≥﹣3时,y随x的增大而增大;(3)x≥1
﹣2;(2)当x≥﹣3时,y随x的增大而增大;(3)x≥1
【解析】
(1)根据在函数y=y=2![]() ﹣b中,根据函数y=2
﹣b中,根据函数y=2![]() ﹣b的定义域为x≥﹣3,当x=0时y=2
﹣b的定义域为x≥﹣3,当x=0时y=2![]() ﹣2,可以求得该函数的表达式;
﹣2,可以求得该函数的表达式;
(2)根据(1)中的表达式可以画出该函数的图象并写出它的一条性质;
(3)根据图象可以直接写出所求不等式的解集.
(1)∵![]() ,
,
∴![]() ,
,
∵函数y=2![]() ﹣b的定义域为
﹣b的定义域为![]() ,
,
∴![]() ,
,
∵当![]() 时,
时,![]() ,
,
∴2![]() ﹣2=2
﹣2=2![]() ﹣b,
﹣b,
∴![]() ,
,
∴函数的解析式为:![]() ;
;
故答案为:y=2![]() ﹣2;
﹣2;
(2)
| -3 | -2 | -1 | 0 | 1 | 2 | 3 |
|
| -2 | 0 | 0.8 | 1.5 | 2 | 2.5 | 2.9 |
|
描点,按顺序连线该函数的图象如下图所示:
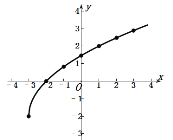
性质是当![]() 时,y随x的增大而增大;
时,y随x的增大而增大;
故答案为:当x≥﹣3时,y随x的增大而增大;
(3)如图,
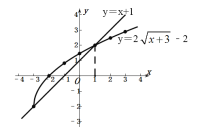
由函数图象可得,
不等式2![]() ﹣b≤x+1的解集是x≥1.
﹣b≤x+1的解集是x≥1.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案【题目】甲、乙两运动员的射击成绩(靶心为10环)统计如下表(不完全):
运动员 \ 环数 \ 次数 | 1 | 2 | 3 | 4 | 5 |
甲 | 10 | 8 | 9 | 10 | 8 |
乙 | 10 | 9 | 9 | a | b |
某同学计算出了甲的成绩平均数是9,方差是![]() =
=![]() [(10-9)2+(8-9)2+(9-9)2+(10-9)2+(8-9)2]=0.8,
[(10-9)2+(8-9)2+(9-9)2+(10-9)2+(8-9)2]=0.8,
请作答:
(1)若甲、乙射击成绩平均数都一样,则a+b= ;
(2)在(1)的条件下,当甲比乙的成绩较稳定时,请列举出a,b的所有可能取值,并说明理由.