题目内容
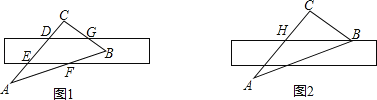
【题目】如图，AB为半圆O的直径，点C在半圆O上，AB＝8，∠CAB＝60°，P是弧
上的一个点，连接AP，过点C作CD⊥AP于点D，连接BD，在点P移动过程中，BD长的最小值为_____．
【答案】2
﹣2
【解析】
以AC为直径作圆O′，连接BO′、BC．在点P移动的过程中，点D在以AC为直径的圆上运动，当O′、D、B共线时，BD的值最小，最小值为O′B﹣O′D，利用勾股定理求出BO′即可解决问题．
解：如图，以AC为直径作圆O′，连接BO′、BC，O'D，
∵CD⊥AP，
∴∠ADC＝90°，
∴在点P移动的过程中，点D在以AC为直径的圆上运动，
∵AB是直径，
∴∠ACB＝90°，
在Rt△ABC中，∵AB＝8，∠CAB＝60°，
∴BC＝ABsin60°＝
，AC＝ABcos60°＝4，
∴AO'＝CO'＝2，
∴BO'＝
∵O′D+BD≥O′B，
∴当O′、D、B共线时，BD的值最小，最小值为O′B﹣O′D＝
故答案为
练习册系列答案
相关题目
【题目】阅读理解 在研究函数
的图象性质时，我们用“描点”的方法画出函数的图象.
列出表示几组
与
的对应值：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
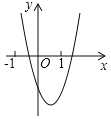
描点连线：以表中各对对应值为坐标，描出各点，并用平滑的曲线顺次连接这些点，就得到函数的图象，如图1：
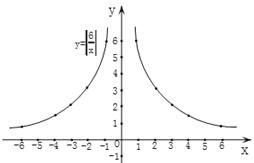
图1
可以看出，这个函数图象的两个分支分别在第一、二象限，且当
时，与函数
在第一象限的图象相同；当
时，与函数
在第二象限的图象相同.类似地，我们把函数
（
是常数，
）的图象称为“并进双曲线”.
认真观察图表，分别写出“并进双曲线”的对称性、函数的增减性性质：
①图象的对称性性质： ；
②函数的增减性性质： ；
延伸探究如图2，点M，N分别在“并进双曲线”的两个分支上，
，判断
与
的数量关系，并说明理由.
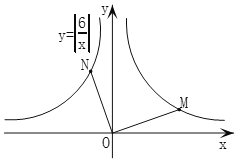
图2
