Question

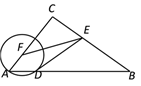
【题目】（1）如图所示，∠B=∠OAF=90°，BO=3cm，AB=4cm，AF=12cm，求图中半圆的面积．

（2）在直角坐标系内，一次函数y=kx+b的图象经过三点A（2，0），B（0，2），C（m，3）．求这个一次函数解析式并求m的值．

Answer 1

【答案】(1)图中半圆的面积是cm2；(2) y=﹣x+2，m=﹣1．

【解析】

(1)首先，在直角△ABO中，利用勾股定理求得AO=5cm；然后在直角△AFO中，由勾股定理求得斜边FO的长度；最后根据圆形的面积公式进行解答；（2）将两个已知点A（2，0），B（0，2）分别代入y=kx+b，分别求出k、b的解析式，再将未知点C（m，3）代入一次函数解析式，求出m的值．

如图，∵在直角△ABO中，∠B=90°，BO=3cm，AB=4cm，

∴AO= =5cm．

则在直角△AFO中，由勾股定理得到：FO= =13cm，

∴图中半圆的面积= （cm2）．

答：图中半圆的面积是cm2．

(2)由已知条件，得 ，

解得 ．

∴一次函数解析式为y=﹣x+2，

∵一次函数y=﹣x+2过C（m，3）点，

∴3=﹣m+2，

∴m=﹣1．