题目内容
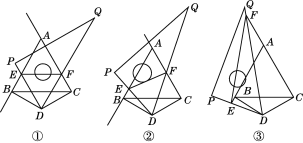
【题目】如图，在梯形ABCD中，AD∥BC，对角线 AC、BD交于点 M，点E在边BC上，且∠DAE=∠DCB，联结AE，AE与BD交于点F．
（1）求证：
；
（2）连接DE，如果BF=3FM，求证：四边形ABED是平行四边形.
【答案】 (1) 证明见解析;(2) 证明见解析.
【解析】分析：（1）由AD∥BC可得出∠DAE=∠AEB，结合∠DCB=∠DAE可得出∠DCB=∠AEB，进而可得出AE∥DC、△AMF∽△CMD，根据相似三角形的性质可得出
=
，根据AD∥BC，可得出△AMD∽△CMB，根据相似三角形的性质可得出=
，进而可得出=，即MD2=MFMB；
（2）设FM=a，则BF=3a，BM=4a．由（1）的结论可求出MD的长度，代入DF=DM+MF可得出DF的长度，由AD∥BC，可得出△AFD∽△△EFB，根据相似三角形的性质可得出AF=EF，利用“对角线互相平分的四边形是平行四边形”即可证出四边形ABED是平行四边形．
详解：（1）∵AD∥BC，∴∠DAE=∠AEB．∵∠DCB=∠DAE，∴∠DCB=∠AEB，∴AE∥DC，∴△AMF∽△CMD，∴=．
∵AD∥BC，∴△AMD∽△CMB，∴=
=，即MD2=MFMB．
（2）设FM=a，则BF=3a，BM=4a．
由MD2=MFMB，得：MD2=a4a，∴MD=2a，∴DF=BF=3a．
∵AD∥BC，∴△AFD∽△△EFB，∴
=
=1，∴AF=EF，∴四边形ABED是平行四边形．
【题目】某食品厂从生产的袋装食品中抽出样品20袋，以每袋标准质量45克为标准，检测每袋的质量是否符合该标准，超过或不足的克数分别用正、负数来表示，记录如下：
与标准质量的差值（单位：克） | ﹣5 | ﹣3 | 0 | 1 | 2 | 5 |
袋数 | 1 | 3 | 6 | 4 | 5 | 1 |
回答下列问题：
（1）这20袋样品中，完全符合每袋标准质量45克的有 袋；
（2）这批样品的总质量是多少克？（要求写出算式）．
