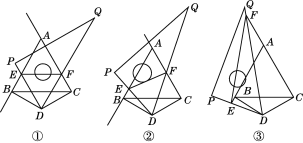
题目内容
【题目】已知:正方形ABCD和等腰直角三角形AEF,AE=AF(AE<AD),连接DE、BF,P是DE的中点,连接AP。将△AEF绕点A逆时针旋转。
(1)如图①,当△AEF的顶点E、F恰好分别落在边AB、AD时,则线段AP与线段BF的位置关系为 ,数量关系为 。
(2)当△AEF绕点A逆时针旋转到如图②所示位置时,证明:第(1)问中的结论仍然成立。
(3)若AB=3,AE=1,则线段AP的取值范围为 。

【答案】(1)AP⊥BF,![]() (2)见解析;(3)1≤AP≤2
(2)见解析;(3)1≤AP≤2
【解析】
(1)根据直角三角形斜边中线定理可得![]() ,即△APD为等腰三角形推出∠DAP=∠EDA,可证△AED≌△ABF可得∠ABF=∠EDA=∠DAP 且 BF=ED由三角形内角和可得∠AOF=90°即AP⊥BF由全等可得
,即△APD为等腰三角形推出∠DAP=∠EDA,可证△AED≌△ABF可得∠ABF=∠EDA=∠DAP 且 BF=ED由三角形内角和可得∠AOF=90°即AP⊥BF由全等可得![]() 即
即![]()
(2)延长AP至Q点使得DQ∥AE,PA延长线交于G点,利用P是DE中点,构造△AEP≌△PDQ可得∠EAP=∠PQD,DQ=AE=FA可得∠QDA=∠FAB可证△FAB≌△QDA 得到∠AFB=∠PQD=∠EAP,AQ=FB由三角形内角和可得∠FAG=90°得出AG⊥FB即AP⊥BF由全等可得![]()
(3)由于![]() 即求BF的取值范围,当BF最小时,即F在AB上,此时BF=2,AP=1
即求BF的取值范围,当BF最小时,即F在AB上,此时BF=2,AP=1
当BF最大时,即F在BA延长线上,此时BF=4,AP=2可得1≤AP≤2
(1)

根据直角三角形斜边中线定理有AP是△AED中线可得![]() ,即△APD为等腰三角形。
,即△APD为等腰三角形。
∴∠DAP=∠EDA
又AE=AF,∠BAF=∠DAE=90°,AB=AD
∴△AED≌△ABF
∴∠ABF=∠EDA=∠DAP 且 BF=ED
设AP与BF相交于点O
∴∠ABF+∠AFB=90°=∠DAP+∠AFB
∴∠AOF=90°即AP⊥BF
∴![]() 即
即![]()
故答案为:AP⊥BF,![]()
(2)

延长AP至Q点使得DQ∥AE,PA延长线交于G点
∴∠EAP=∠PQD,∠AEP=∠QDP
∵P是DE中点,
∴EP=DP
∴△AEP≌△PDQ
则∠EAP=∠PQD,DQ=AE=FA
∠QDA=180°-(∠PAD+∠PQD)
=180°-∠EAD
而∠FAB=180°-∠EAD,则∠QDA=∠FAB
∵AF=DQ,∠QDA=∠FAB ,AB=AD
∴△FAB≌△QDA
∴∠AFB=∠PQD=∠EAP,AQ=FB
而∠EAP+∠FAG=90°
∴∠AFB+∠FAG=90°
∴∠FAG=90°
∴AG⊥FB
即AP⊥BF
又![]()
∴![]()
(3)∵![]()
∴即求BF的取值范围
BF最小时,即F在AB上,此时BF=2,AP=1
BF最大时,即F在BA延长线上,此时BF=4,AP=2
∴ 1≤AP≤2

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案【题目】某同学上学期的数学历次测验成绩如下表所示:
测验类别 | 平时测验 | 期中测验 | 期末测验 | ||
第1次 | 第2次 | 第3次 | |||
成绩 | 100 | 106 | 106 | 105 | 110 |
(1)该同学上学期5次测验成绩的众数为 ,中位数为 ;
(2)该同学上学期数学平时成绩的平均数为 ;
(3)该同学上学期的总成绩是将平时测验的平均成绩、期中测验成绩、期末测验成绩按照2:3:5的比例计算所得,求该同学上学期数学学科的总评成绩(结果保留整数)。
【题目】某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
(1)根据图示填写下表:
平均数/分 | 中位数/分 | 众数/分 | |
A校 | ______ | 85 | ______ |
B校 | 85 | ______ | 100 |
(2)结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
(3)计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.