题目内容
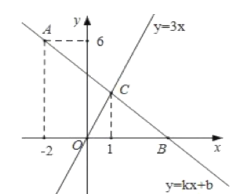
【题目】如图,二次函数y=―ax2+2ax+c(a>0)的图象交x轴于A、B两点,交y轴于点C,过A的直线y=kx+2k(k≠0)与这个二次函数图象交于另一点F,与其对称轴交于点E,与y轴交于点D,且DE=EF.
(1)求A点坐标;
(2)若△BDF的面积为12,求此二次函数的表达式;
(3)设二次函数图象顶点为P,连接PF,PC,若∠CPF=2∠DAB,求此二次函数的表达式.

【答案】(1) A(2,0);(2) y=x+2x+8;(3) y=![]() x+
x+![]() x+4
x+4![]() .
.
【解析】分析:(1)求出一次函数值为0时对应的自变量的值可得到A点坐标;
(2)利用二次函数的性质得到抛物线的对称轴为直线x=1,则利用对称性得到B点坐标为(4,0),把A点坐标代入得c=8a,则抛物线解析式为y=﹣ax2+2ax+8a,再根据DE=EF可确定F(2,8a),接着把F(2,8a)代入一次函数得到y=kx+2k得k=2a,所以D(0,4a),然后利用三角形面积公式得到![]() (4+2)8a﹣
(4+2)8a﹣![]() (4+2)4a=12,于是解方程求出a,从而得到抛物线解析式;
(4+2)4a=12,于是解方程求出a,从而得到抛物线解析式;
(3)利用抛物线的解析式为y=﹣ax2+2ax+8a得到C(0,8a),P(1,9a),则可判断CF∥x轴,所以E(1,8a),根据二次函数的对称性判断△PCF为等腰三角形,则∠CPF=2∠CPE,于是可证明∠DAB=∠CPE,然后根据相似三角形的判定方法可得到Rt△ADO∽Rt△PCE,再利用相似比可其求出a的值,从而得到抛物线解析式.
详解:(1)当y=0时,kx+2k=0,解得:x=﹣2,则A(﹣2,0);
(2)∵二次函数y=﹣ax2+2ax+c(a>0)的图象的对称轴为直线x=﹣![]() =1,∴B点坐标为(4,0),把A(﹣2,0)代入y=﹣ax2+2ax+c得:﹣4a﹣4a+c=0,∴c=8a,∴抛物线解析式为y=﹣ax2+2ax+8a.∵DE=EF,∴F点的横坐标为2,∴F(2,8a),把F(2,8a)代入y=kx+2k得8a=2k+2k,解得:k=2a,∴y=2ax+4a,当x=0时,y=4a,则D(0,4a).∵S△BDF=S△FAB﹣S△DAB,∴
=1,∴B点坐标为(4,0),把A(﹣2,0)代入y=﹣ax2+2ax+c得:﹣4a﹣4a+c=0,∴c=8a,∴抛物线解析式为y=﹣ax2+2ax+8a.∵DE=EF,∴F点的横坐标为2,∴F(2,8a),把F(2,8a)代入y=kx+2k得8a=2k+2k,解得:k=2a,∴y=2ax+4a,当x=0时,y=4a,则D(0,4a).∵S△BDF=S△FAB﹣S△DAB,∴![]() (4+2)8a﹣
(4+2)8a﹣![]() (4+2)4a=12,解得:a=1,∴抛物线解析式为y=﹣x2+2x+8;
(4+2)4a=12,解得:a=1,∴抛物线解析式为y=﹣x2+2x+8;
(3)抛物线的解析式表示为y=﹣ax2+2ax+8a,D(0,4a),F(2,8a),当x=0时,y=﹣ax2+2ax+8a=8a,则C(0,8a),当x=1时,y=﹣ax2+2ax+8a=9a,则P(1,9a).∵F(2,8a),C(0,8a),∴CF∥x轴,E(1,8a),∴△PCF为等腰三角形,∴PE平分∠CPF,即∠CPF=2∠CPE.∵∠CPF=2∠DAB,∴∠DAB=∠CPE,∴Rt△ADO∽Rt△PCE,∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得:a=
,解得:a=![]() 或a=﹣
或a=﹣![]() (舍去),∴抛物线的解析式表示为y=﹣
(舍去),∴抛物线的解析式表示为y=﹣![]() x2+
x2+![]() x+4
x+4![]() .
.
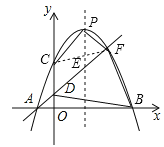

【题目】某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
(1)根据图示填写下表:
平均数/分 | 中位数/分 | 众数/分 | |
A校 | ______ | 85 | ______ |
B校 | 85 | ______ | 100 |
(2)结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
(3)计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.

【题目】在汛期来临之前,某市提前做好防汛工作,该市的![]() 、
、![]() 两乡镇急需防汛物质分别为80吨和120吨,由该市的甲、乙两个地方负责全部运送到位,甲、乙两地有防汛物质分别为110吨和90吨,已知甲、乙两地运到
两乡镇急需防汛物质分别为80吨和120吨,由该市的甲、乙两个地方负责全部运送到位,甲、乙两地有防汛物质分别为110吨和90吨,已知甲、乙两地运到![]() 、
、![]() 两乡镇的每吨物质的运费如表所示:
两乡镇的每吨物质的运费如表所示:
甲 | 乙 | |
| 20元/吨 | 15元/吨 |
| 25元/吨 | 24元/吨 |
(1)设乙地运到![]() 乡镇的防汛物质为
乡镇的防汛物质为![]() 吨,求总运费
吨,求总运费![]() (元)关于
(元)关于![]() (吨)的函数关系式,并指出
(吨)的函数关系式,并指出![]() 的取值范围.
的取值范围.
(2)求最低总运费,并说明总运费最低时的运送方案.