题目内容
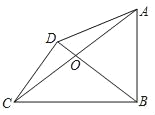
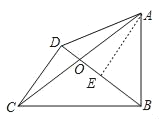
【题目】如图,在四边形ABCD中,∠ABC=90°,对角线AC、BD交于点O,AO=CO,CD⊥BD,如果CD=3,BC=5,那么AB=_____.
【答案】![]()
【解析】
过点A作AE⊥BD,由AAS得△AOE≌△COD,从而得CD=AE=3,由勾股定理得DB=4,易证△ABE∽△BCD,得![]() ,进而即可求解.
,进而即可求解.
过点A作AE⊥BD,
∵CD⊥BD,AE⊥BD,
∴∠CDB=∠AED=90°,CO=AO,∠COD=∠AOE,
∴△AOE≌△COD(AAS)
∴CD=AE=3,
∵∠CDB=90°,BC=5,CD=3,
∴DB=![]() =4,
=4,
∵∠ABC=∠AEB=90°,
∴∠ABE+∠EAB=90°,∠CBD+∠ABE=90°,
∴∠EAB=∠CBD,
又∵∠CDB=∠AEB=90°,
∴△ABE∽△BCD,
∴![]() ,
,
∴![]() ,
,
∴AB=![]() .
.
故答案为:![]() .
.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目