Question

【题目】问题：如果α，β都为锐角，且tanα＝，tanβ＝，求α+β的度数．

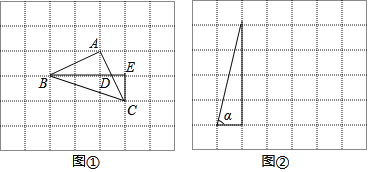
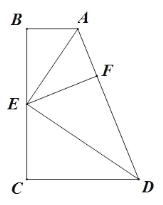
解决：如图①，把α，β放在正方形网格中，使得∠ABD＝α，∠CBE＝β，连结AC，易证△ABC是等腰直角三角形，因此可求得α+β＝∠ABC＝　 　．

拓展：参考以上方法，解决下列问题：如果α，β都为锐角，当tanα＝4，tanβ＝时，

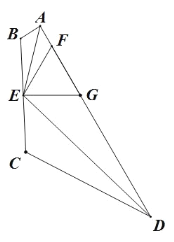
（1）在图②的正方形网格中，利用已作出的锐角α，画出∠MON＝α﹣β；

（2）求出α﹣β＝　 　°．

Answer 1

【答案】解决：45°；拓展：（1）见解析；（2）45

【解析】

解决：观察图象①可知：△ABC是等腰直角三角形，由此即可解决问题；

拓展：（1）模仿例题，构造∠ABE＝α，∠DBC＝β，使tanα＝4，tanβ＝ ，从而构造出∠MON；

（2）证出等腰直角三角形即可解决问题．

解：解决：观察图象①，根据勾股定理可得AB=，AC=，BC=

∴AB=AC，AB2＋ AC2= BC2

∴△ABC是等腰直角三角形．

∴α+β＝∠ABC＝45°，

故答案为45°．

拓展：（1）如图②中，∠MOE＝α，∠NOC＝β，使tanα＝4，tanβ＝ ，连接MN

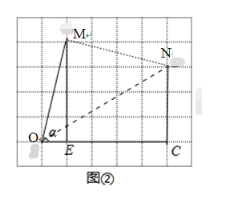
∴α﹣β＝∠MON，∠MON即为所求；

（2）根据勾股定理可得MO=，MN=，ON=

∴MO=MN，MO2＋MN= ON2

∵△MON是等腰直角三角形，

∴∠MON＝45°，

∴α﹣β＝45°．

故答案为45．