题目内容
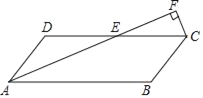
【题目】如图,四边形ABCD为平行四边形,AD=1,AB=3,∠DAB=60°,点E为边CD上一动点,过点C作AE的垂线交AE的延长线于点F.
(1)求∠D的度数;
(2)若点E为CD的中点,求EF的值;
(3)当点E在线段CD上运动时,![]() 是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
【答案】(1)∠ADC=120°;(2)EF=![]() ,(3)有最大值,最大值为:
,(3)有最大值,最大值为:![]()
【解析】
(1)由四边形ABCD是平行四边形,得AB∥CB,进而即可得到答案;
(2)作AH⊥CD交CD的延长线于H,由在Rt△ADH中,∠H=90°,∠ADH=60°,得A=![]() ,DH=
,DH=![]() ,结合勾股定理得AE=
,结合勾股定理得AE=![]() ,易证△AEH∽△CEF,得
,易证△AEH∽△CEF,得![]() ,进而即可求解;
,进而即可求解;
(3)作△AFC的外接圆⊙O,作AH⊥CD交CD的延长线于H,作OK⊥CD于K,交⊙O于M,作FP∥CD交AD的延长线于P,作MN∥CD交AD的延长线于N,作NQ⊥CD于Q.易得PA的值最大时,![]() 的值最大,PA的值最大=AN的长,根据勾股定理和三角函数的定义得DN=
的值最大,PA的值最大=AN的长,根据勾股定理和三角函数的定义得DN=![]() ,从而得AN=AD+DN=
,从而得AN=AD+DN=![]() ,进而即可得到答案.
,进而即可得到答案.
(1)∵四边形ABCD是平行四边形,
∴AB∥CB,
∴∠ADC+∠DAB=180°,
∵∠DAB=60°,
∴∠ADC=120°.
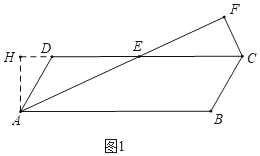
(2)作AH⊥CD交CD的延长线于H,如图1,
∵在Rt△ADH中,∠H=90°,∠ADH=60°,AD=2,
∴AH=ADsin60°=![]() ,DH=ADcos60°=
,DH=ADcos60°=![]() ,
,
∵DE=EC=![]() ,
,
∴EH=DH+DE=2,
∴AE=![]() ,
,
∵CF⊥AF,
∴∠F=∠H=90°,
∵∠AEH=∠CEF,
∴△AEH∽△CEF,
∴![]() ,
,
∴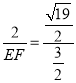 ,
,
∴EF=![]() .
.
(3)如图2中,作△AFC的外接圆⊙O,作AH⊥CD交CD的延长线于H,作OK⊥CD于K,交⊙O于M,作FP∥CD交AD的延长线于P,作MN∥CD交AD的延长线于N,作NQ⊥CD于Q.
∵DE∥PF,
∴![]() ,
,
∵AD是定值,
∴PA的值最大时,![]() 的值最大,
的值最大,
观察图形可知,当点F与点M重合时,PA的值最大,最大值=AN的长,
由(2)可知,AH=![]() ,CH=
,CH=![]() ,∠H=90°,
,∠H=90°,
∴AC=![]() ,
,
∴OM=![]() AC=
AC=![]() ,
,
∵OK∥AH,AO=OC,
∴KH=KC,
∴OK=![]() =
=![]() ,
,
∴MK=NQ=![]() ﹣
﹣![]() ,
,
在Rt△NDQ中,DN= ,
,
∴AN=AD+DN=![]() ,
,
∴![]() 的最大值=
的最大值=![]() =
=![]() .
.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案