题目内容
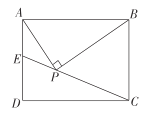
【题目】已知，将矩形ABCD折叠，使点C与点A重合，点D落在点G处，折痕为EF．
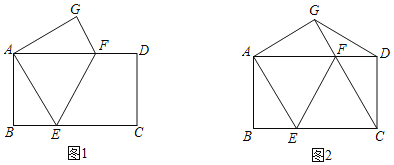
（1）如图1，求证：BE＝GF；
（2）如图2，连接CF、DG，若CE＝2BE，在不添加任何辅助线的情况下，请直接写出图2中的四个三角形，使写出的每个三角形都为等腰三角形
【答案】（1）见解析；（2）△CEF，△AGD，△FGD，△DGC，△AEF是等腰三角形．
【解析】
（1）根据题意，通过证明
即可得到
；
（2）根据题意将矩形ABCD折叠，使点C与点A重合，点D落在点G处，通过等腰三角形的判定及性质即可得到
是等腰三角形.
（1）证明∵矩形ABCD
∴
由折叠可知：
∴
∴
，且
∴
∴；
（2）证明：∵将矩形ABCD折叠，使点C与点A重合，点D落在点G处
∴
∴
是等腰三角形
∵
∴
∴
∴
∴
是等腰三角形
∵
∴
，且
∴
∴
∵
∴
∴
∴
∴
∴
∴
是等腰三角形
综上所述：是等腰三角形．
练习册系列答案
相关题目
