Question

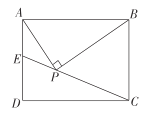
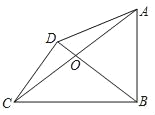
【题目】如图，已知AB＝10，以AB为直径作半圆O，半径OA绕点O顺时针旋转得到OC，点A的对应点为C，当点C与点B重合时停止．连接BC并延长到点D，使得CD＝BC，过点D作DE⊥AB于点E，连接AD，AC．

（1）AD＝　 　；

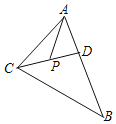
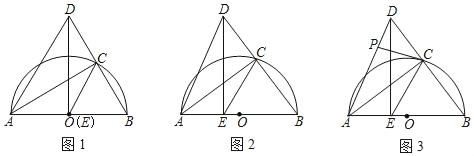
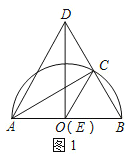
（2）如图1，当点E与点O重合时，判断△ABD的形状，并说明理由；

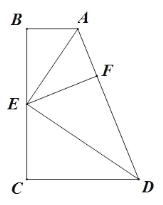
（3）如图2，当OE＝1时，求BC的长；

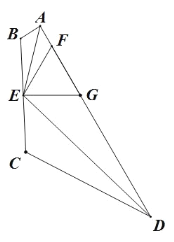
（4）如图3，若点P是线段AD上一点，连接PC，当PC与半圆O相切时，直接写出直线PC与AD的位置关系．

Answer 1

【答案】（1）10；（2）（2）△ABD是等边三角形，理由详见解析；（3）BC的长为或2；（4）PC⊥AD，理由详见解析

【解析】

（1）由圆周角定理得到，结合已知条件和等腰三角形“三线合一”性质推知；

（2）是等边三角形．理由：由等腰 “三线合一”性质得到；又由（1）的结论可以推知，即是等边三角形；

（3）分类讨论：点在线段和线段上，借助于勾股定理求得的长度；

（4）由三角形中位线定理知，又由切线的性质知，所以根据平行线的性质推知．

解：（1）是圆的直径，

．

又，

．

故答案是：10；

（2）是等边三角形，

理由如下：如图1，

点与点重合，

，

，

，

，

，

是等边三角形；

（3）如图2，

，

，

当点在上时，

则，，

，，

在和中，

由勾股定理得，即，

解得，

；

当点在上时，同理可得，

解得，

，

综上所述，的长为或；

（4）．理由如下：

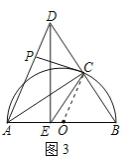
如图3，连接．

点是的中点，点是的中点，

是的中位线，

．

又与半圆相切，

，

．