题目内容
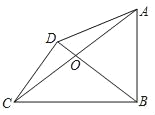
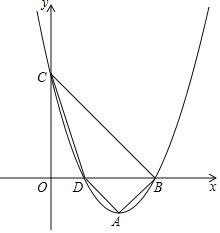
【题目】如图,已知二次函数y=x2﹣4x+3图象与x轴分别交于点B、D,与y轴交于点C,顶点为A,分别连接AB,BC,CD,DA.
(1)求四边形ABCD的面积;
(2)当y>0时,自变量x的取值范围是 .
【答案】(1)4;(2)x>3或x<1.
【解析】
(1)四边形ABCD的面积=![]() ×BD×(xC﹣xA)=
×BD×(xC﹣xA)=![]() ×2×(3+1)=4;
×2×(3+1)=4;
(2)从图象可以看出,当y>0时,自变量x的取值范围是:x>3或x<1,即可求解.
(1)函数y=x2﹣4x+3图象与x轴分别交于点B、D,与y轴交于点C,顶点为A,
则点B、D、C、A的坐标分别为:(3,0)、(1,0)、(0,3)、(2,﹣1);
四边形ABCD的面积=![]() ×BD×(xC﹣xA)=
×BD×(xC﹣xA)=![]() ×2×(3+1)=4;
×2×(3+1)=4;
(2)从图象可以看出,当y>0时,自变量x的取值范围是:x>3或x<1,
故答案为:x>3或x<1.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目