题目内容
【题目】定义:如果三角形的两个内角∠α与∠β满足∠α=2∠β,那么,我们将这样的三角形称为“倍角三角形”.如果一个等腰三角形是“倍角三角形”,那么这个等腰三角形的腰长与底边长的比值为____.
【答案】![]() 或
或![]() .
.
【解析】
若等腰三角形的三个内角![]() 、
、![]() ,
,![]() ,利用
,利用![]() 和
和![]() 得
得![]() ,此“倍角三角形”为等腰直角三角形,从而得到腰长与底边长的比值;若等腰三角形的三个内角
,此“倍角三角形”为等腰直角三角形,从而得到腰长与底边长的比值;若等腰三角形的三个内角![]() 、
、![]() ,
,![]() ,利用
,利用![]() 和
和![]() 得
得![]() ,如图,
,如图,![]() ,
,![]() ,作
,作![]() 的平分线
的平分线![]() ,则
,则![]() ,易得
,易得![]() ,再证明
,再证明![]() ,利用相似比得到
,利用相似比得到![]() ,等量代换得到
,等量代换得到![]() ,然后解关于
,然后解关于![]() 的方程
的方程![]() 得
得![]() 与
与![]() 的比值即可.
的比值即可.
解:若等腰三角形的三个内角![]() 、
、![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,解得
,解得![]() ,
,
![]() 此“倍角三角形”为等腰直角三角形,
此“倍角三角形”为等腰直角三角形,
![]() 腰长与底边长的比值为
腰长与底边长的比值为![]() ;
;
若等腰三角形的三个内角![]() 、
、![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,解得
,解得![]() ,
,
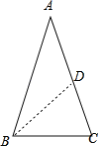
如图,![]() ,
,![]() ,作
,作![]() 的平分线
的平分线![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
即![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
即![]() ,
,
整理得![]() ,解得
,解得![]() ,
,
即![]() ,
,
此时腰长与底边长的比值为![]() ,
,
综上所述,这个等腰三角形的腰长与底边长的比值为![]() 或
或![]() .
.
故答案为![]() 或
或![]() .
.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目