题目内容
【题目】如图,△ABC是⊙O的内接三角形.AE是⊙O的直径,交BC于点G.过点A作AF⊥BC,AF分别与BC、⊙O交于点D、F,连接BE、CF.
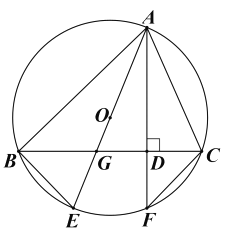
(1)求证:∠BAE=∠CAF;
(2)若AB=8,AC=6,AG=5,求AF的长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)由圆周角定理得出∠ABE=90°,得出∠BAE+∠BEA=90°,由AF⊥BC得出∠ACD+∠CAF =90°,由圆周角定理得出∠BEA=∠ACD,即可得出结论;
(2)先证明∠ABC=∠AFC,∠BAE=∠CAF得△ABG∽△AFC,得到![]() 即可得到答案.
即可得到答案.
解(1)∵AE是⊙O的直径,
∴∠ABE=90°,
∴∠BAE+∠BEA=90°,
∵AF⊥BC,
∴∠ADC=90°,
∴∠ACD+∠CAF =90°,
又∵∠BEA=∠ACD,
∴∠BAE=∠CAF;
(2)∵∠ABC与∠AFC是![]() 的圆周角
的圆周角
∴∠ABC=∠AFC
∵∠BAE=∠CAF
∴△ABG∽△AFC
∴![]()
∵AB=8,AC=6,AG=5
∴![]() 得
得![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某单位计划购进![]() 三种型号的礼品共
三种型号的礼品共![]() 件,其中
件,其中![]() 型号礼品
型号礼品![]() 件,
件,![]() 型号礼品比
型号礼品比![]() 型号礼品多
型号礼品多![]() 件.已知三种型号礼品的单价如下表:
件.已知三种型号礼品的单价如下表:
型号 |
|
|
|
单价(元/件) |
|
|
|
(1)求计划购进![]() 和
和![]() 两种型号礼品分别多少件?
两种型号礼品分别多少件?
(2)实际购买时,厂家给予打折优惠销售(如: ![]() 折指原价
折指原价![]() ,在计划总价额不变的情况下,准备购进这批礼品.
,在计划总价额不变的情况下,准备购进这批礼品.
①若只购进![]() 两种型号礼品,且
两种型号礼品,且![]() 型礼品件数不超过
型礼品件数不超过![]() 型礼品的
型礼品的![]() 倍,求
倍,求![]() 型礼品最多购进多少件?
型礼品最多购进多少件?
②若只购进![]() 两种型号礼品,它们的单价分别打
两种型号礼品,它们的单价分别打![]() 折、
折、![]() 折,
折,![]() 均为整数,且购进的礼品总数比计划多
均为整数,且购进的礼品总数比计划多![]() 件,求
件,求![]() 的值.
的值.