题目内容
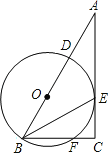
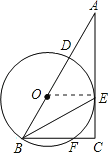
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.
【答案】(1)详见解析;(2)4
【解析】
(1)首先利用等腰三角形的性质和角平分线的定义得出∠EBC=∠OEB,然后得出OE∥BC,则有∠OEA=∠ACB=90°,则结论可证.
(2)连接OE、OF,过点O作OH⊥BF交BF于H,首先证明四边形OHCE是矩形,则有![]() ,然后利用等腰三角形的性质求出BH的长度,再利用勾股定理即可求出OH的长度,则答案可求.
,然后利用等腰三角形的性质求出BH的长度,再利用勾股定理即可求出OH的长度,则答案可求.
(1)证明:连接OE.
∵OE=OB,
∴∠OBE=∠OEB.
∵BE平分∠ABC,
∴∠OBE=∠EBC,
∴∠EBC=∠OEB,
∴OE∥BC,
∴∠OEA=∠ACB.
∵∠ACB=90°,
∴∠OEA=90°
∴AC是⊙O的切线;
(2)解:连接OE、OF,过点O作OH⊥BF交BF于H,

∵OH⊥BF,
![]() .
.
![]()
∴四边形OECH为矩形,
∴OH=CE.
∵![]() ,BF=6,
,BF=6,
∴BH=3.
在Rt△BHO中,OB=5,
∴OH=![]() =4,
=4,
∴CE=4.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案
相关题目
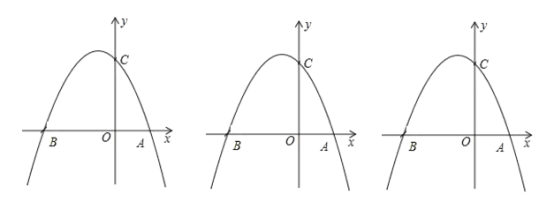
【题目】已知二次函数![]() 的
的![]() 与
与![]() 的部分对应值如表:
的部分对应值如表:
|
|
|
|
|
|
|
|
|
|
|
|
下列结论:![]() 抛物线的开口向上;②抛物线的对称轴为直线
抛物线的开口向上;②抛物线的对称轴为直线![]() ;③当
;③当![]() 时,
时,![]() ;④抛物线与
;④抛物线与![]() 轴的两个交点间的距离是
轴的两个交点间的距离是![]() ;⑤若
;⑤若![]() 是抛物线上两点,则
是抛物线上两点,则![]() ,其中正确的个数是( )
,其中正确的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()