Question

【题目】如图，已知⊙O的半径为6，点A、B在⊙O上，∠AOB＝60°，动点C在⊙O上（与A、B两点不重合），连接BC，点D是BC中点，连接AD，则线段AD的最大值为_____．

Answer 1

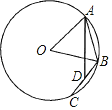
【答案】3

【解析】

取OB中点E得DE是△OBC的中位线，知DE＝OC＝3，即点D是在以E为圆心，3为半径的圆上，从而知求AD的最大值就是求点A与⊙E上的点的距离的最大值，据此求解可得．

解：如图，连接OC，Q取OB的中点E，连接DE．

则OE＝EB＝OB＝3，

在△OBC中，DE是△OBC的中位线，

∴DE＝OC＝3，

∴EO＝ED＝EB，

即点D是在以E为圆心，2为半径的圆上，

∴求AD的最大值就是求点A与⊙E上的点的距离的最大值，

如图，当D在线段AE延长线上时，AD取最大值，

∵OA＝OB＝6，∠AOB＝60°，OE＝EB，

∴AE＝3，DE＝3，

∴AD取最大值为3+3．

故答案为3．