题目内容
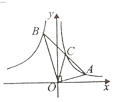
【题目】如图,点![]() 在反比例函数
在反比例函数![]() 的图象上,点
的图象上,点![]() 在反比例函数
在反比例函数![]() 的图象上,且
的图象上,且![]() ,线段
,线段![]() 交反比例函数
交反比例函数![]() 的图象于另一点
的图象于另一点![]() ,连结
,连结![]() .若点
.若点![]() 为
为![]() 的中点,
的中点,![]() ,则
,则![]() 的值为_________.
的值为_________.
【答案】![]()
【解析】
过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,由tan∠OCA=![]() ,得∠OCA=60°,再由直角三角形斜边上的中线等于斜边的一半可得出OC=AC,进而可得出△AOC为等边三角形,进而求得
,得∠OCA=60°,再由直角三角形斜边上的中线等于斜边的一半可得出OC=AC,进而可得出△AOC为等边三角形,进而求得![]() ,再证明△AOD∽△OBE,根据相似三角形的性质结合反比例函数k的几何意义可得出结果.
,再证明△AOD∽△OBE,根据相似三角形的性质结合反比例函数k的几何意义可得出结果.
解:过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,如图所示.
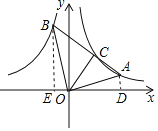
∵tan∠OCA=![]() ,
,
∴∠OCA=60°,
∵∠AOB=90°,点C为AB的中点,
∴OC=AC=BC,
∴△OAC是等边三角形,
∴∠OAB=60°,
∴![]() =
=![]()
∵∠AOB=90°,
∴∠AOD+∠BOE=90°,
∵∠AOD+∠OAD=90°,
∴∠OAD=∠BOE,
∵∠ADO=∠OEB=90°,
∴△AOD∽△OBE,
∴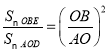 =3.
=3.
∵点A在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴S△AOD=![]()
∴S△OBE=![]() .
.
∵点B在反比例函数y=![]() (k<0)的图象上,
(k<0)的图象上,
∴k=﹣![]() =﹣3,
=﹣3,
故答案为:﹣3.

【题目】某单位计划购进![]() 三种型号的礼品共
三种型号的礼品共![]() 件,其中
件,其中![]() 型号礼品
型号礼品![]() 件,
件,![]() 型号礼品比
型号礼品比![]() 型号礼品多
型号礼品多![]() 件.已知三种型号礼品的单价如下表:
件.已知三种型号礼品的单价如下表:
型号 |
|
|
|
单价(元/件) |
|
|
|
(1)求计划购进![]() 和
和![]() 两种型号礼品分别多少件?
两种型号礼品分别多少件?
(2)实际购买时,厂家给予打折优惠销售(如: ![]() 折指原价
折指原价![]() ,在计划总价额不变的情况下,准备购进这批礼品.
,在计划总价额不变的情况下,准备购进这批礼品.
①若只购进![]() 两种型号礼品,且
两种型号礼品,且![]() 型礼品件数不超过
型礼品件数不超过![]() 型礼品的
型礼品的![]() 倍,求
倍,求![]() 型礼品最多购进多少件?
型礼品最多购进多少件?
②若只购进![]() 两种型号礼品,它们的单价分别打
两种型号礼品,它们的单价分别打![]() 折、
折、![]() 折,
折,![]() 均为整数,且购进的礼品总数比计划多
均为整数,且购进的礼品总数比计划多![]() 件,求
件,求![]() 的值.
的值.
【题目】攀枝花得天独厚,气候宜人,农产品资源极为丰富,其中晚熟芒果远销北上广等大城市.某水果店购进一批优质晚熟芒果,进价为10元/千克,售价不低于15元/千克,且不超过40元/每千克,根据销售情况,发现该芒果在一天内的销售量![]() (千克)与该天的售价
(千克)与该天的售价![]() (元/千克)之间的数量满足如下表所示的一次函数关系.
(元/千克)之间的数量满足如下表所示的一次函数关系.
销售量 | … | 32.5 | 35 | 35.5 | 38 | … |
售价 | … | 27.5 | 25 | 24.5 | 22 | … |
(1)某天这种芒果售价为28元/千克.求当天该芒果的销售量
(2)设某天销售这种芒果获利![]() 元,写出
元,写出![]() 与售价
与售价![]() 之间的函数关系式.如果水果店该天获利400元,那么这天芒果的售价为多少元?
之间的函数关系式.如果水果店该天获利400元,那么这天芒果的售价为多少元?