��Ŀ����
����Ŀ�����һ���ı��εĶԽ��߰��ı��ηֳ����������Σ�һ���ǵȱ������Σ���һ���ǸöԽ������ԵĽ�Ϊ60���������Σ����ǰ������Խ��߽�������ı��ε�����Խ��ߣ�����ı��γ�Ϊ�����ı��Σ�
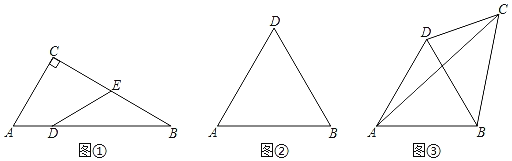
(1)��ͼ�٣���Rt��ABC�С�C=90������B=30����AC=4��DΪAB��һ�㣬AD=2��EΪBC�е㣬����DE����֤���ı���ADECΪ�����ı��Σ�
(2)��ͼ�ڣ���ABC�ǵȱ������Σ���BDΪ����Խ��ߣ��ı���ABCDΪ�����ı��Σ��뻭ͼ�ҳ�����������C������������ͼ���ϣ�
(3)��(2)�������£�
������BCDΪֱ�������Σ�BC=3����AC�ij��ȣ�
����ͼ�ۣ���CD=x��BC=y��AC=z����ֱ��д��x��y��z֮���������ϵ��
���𰸡�(1)��������(2)��������(3)��![]() ��
��![]() ����x2+xy+y2=z2 �����ɼ�����
����x2+xy+y2=z2 �����ɼ�����
��������
(1) ����CD��֤����ACB�ס�ADC���Ƴ���ADC=��ACB=90������֤����CDE�ǵȱ������μ��ɣ�
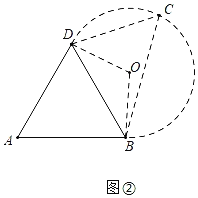
(2)��ͼ���У�������������ODB��ʹ��OD=OB����DOB=120������OΪԲ�ģ�ODΪ�뾶����O������C�ڻ�BCD��ʱ����DCB=![]() ��DOB=60��������������
��DOB=60��������������
(3)�����������Σ���ͼ����1�У�����CDB=90��ʱ����ͼ����2�У�����CBD=90��ʱ���ֱ����ù��ɶ�����⼴�ɣ�
����CDΪ�����ȱ���ECD������BE����EF��BC��BC���ӳ�����F������ȫ�������ε������Լ����ɶ����ɵý��ۣ�
(1)֤������ͼ1�У�����CD��
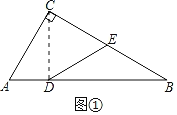
�ߡ�ACB=90����AC=4����B=30����
��AB=2AC=8��
��![]() ��
��![]() ��
��
��![]() ��
��
�ߡ�A=��A��
���ACB�ס�ADC��
���ADC=��ACB=90����
��EC=EB��
��DE=EC=EB��
�ߡ�B=30����
��BC=2CD��
��CD=DE=EC��
���CDE�ǵȱ������Σ�
�ߡ�A=60����
���ı���ADECΪ�����ı��Σ�
(2)�⣺��ͼ���У�������������ODB��ʹ��OD=OB����DOB=120������OΪԲ�ģ�ODΪ�뾶����O������C�ڻ�BCD��ʱ����DCB=![]() ��DOB=60��������������
��DOB=60��������������
(3)�⣺����ͼ����1�У�����CDB=90��ʱ��
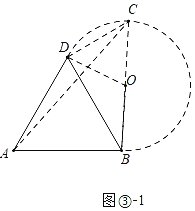
�ߡ�CDB=90������BCD=60����BC=3��
��BD=BCsin6��=![]() ����CBD=30����
����CBD=30����
�ߡ�ABD�ǵȱ������Σ�
��AB=BD=![]() ����ABD=60����
����ABD=60����
���ABC=90����
��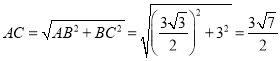 ��
��
![]() ��
��
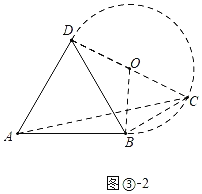
����������AC��ֵΪ![]() ��
��![]() ��
��
����ͼ���У����ۣ�x2+xy+y2=z2��

���ɣ���CDΪ�����ȱ���ECD������BE����EF��BC��BC���ӳ�����F��
�ߡ�EDC=��ADB=60����
���EDB=��CDA��
��ED=CD��BD=AD��
���EDB�ա�CDA(SAS)��
��AC=BE=z��
�ߡ�ECD=��DCB=60����CD=CE=x��
���ECF=60������CEF=30����
��CF=![]() EC=
EC=![]() x��EF=
x��EF=![]() CF=
CF=![]() x��
x��
��Rt��EFB����BE2=EF2+BF2��
��z2=(![]() x)2+(y+
x)2+(y+![]() x)2��
x)2��
�����ã�x2+xy+y2=z2��

����Ŀ��Ϊ���ﴫͳ�Ļ���ijУ��չ�������о����Ļ����Ķ��������������Ϊ�˽��ߡ����꼶ѧ��(�ߡ����꼶����600��ѧ��)���Ķ�Ч������У�����˾����Ļ�֪ʶ�������ִ������꼶�������ȡ20��ѧ���ľ����ɼ�(�ٷ���)���з������������£�
�ռ����ݣ�
���꼶��79��85��73��80��75��76��87��70��75��94��75��79��81��71��75��80��86��59��83��77��
���꼶��92��74��87��82��72��81��94��83��77��83��80��81��71��81��72��77��82��80��70��41��
�������ݣ�
|
|
|
|
|
| |
���꼶 | 0 | 1 | 0 | a | 7 | 1 |
���꼶 | 1 | 0 | 0 | 7 | b | 2 |
�������ݣ�
ƽ���� | ���� | ��λ�� | |
���꼶 | 78 | 75 |
|
���꼶 | 78 |
| 80.5 |
Ӧ�����ݣ�
(1)���ϱ���գ�a= ��b= ��c= ��d= ��
(2)���Ƹ�У�ߡ��������꼶ѧ���ڱ��ξ����гɼ���90�����ϵĹ��ж����ˣ�
(3)����Ϊ�ĸ��꼶��ѧ���Ծ����Ļ�֪ʶ���յ�����ˮƽ�Ϻã���˵�����ɣ�