Question

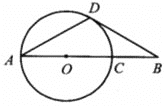
【题目】如图，线段AB经过圆心O，交⊙O于点A、C，点D在⊙O上，连接AD，BD，∠A=∠B=30°．

证明：（1）BD是⊙O的切线

（2）如果BD=2求OC的长

Answer 1

【答案】（1）见解析 （2）

【解析】

试题（1）连接OD，根据∠A和∠B的度数求出∠ADB的度数，然后根据OA=OD求出∠ODA的度数，从而可以得到∠ODB的度数；（2）根据△BOD为直角三角形和BD的长度，求出OD的长度，然后OC=OD求出OC的长度.

试题解析：（1）连接OD ∵OA=OD ∴∠ODA=∠A=30°

∵∠A=∠B=30° ∴∠ADB=180°－30°－30°=120° ∴∠ODB=120°－30°=90°

∴BD是⊙O的切线.

（2）∵∠BDO=90° ∠B=30° BD=2 ∴OD=∴OC=OD=.