题目内容
【题目】已知,如图,直线l经过A(4,0)和B(0,4)两点,抛物线y=a(x﹣h)2的顶点为P(1,0),直线l与抛物线的交点为M.
(1)求直线l的函数解析式;
(2)若S△AMP=3,求抛物线的解析式.
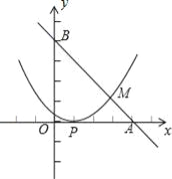
【答案】(1)y=﹣x+4;(2)y=2(x﹣1)2.
【解析】
(1)根据交点坐标先求直线l的函数解析式(2)抛物线的顶点坐标已知,设交点M的坐标,再根据S△AMP=3求出M的坐标,最后求出解析式.
(1)设一次函数解析式为y=kx+b,
把A(4,0),B(0,4)分别代入解析式得![]()
解得![]()
解析式为y=﹣x+4.
(2)设M点的坐标为(m,n),
∵S△AMP=3,
∴![]() (4﹣1)n=3,
(4﹣1)n=3,
解得,n=2,
把M(m,2)代入为2=﹣m+4得,m=2,
M(2,2),
∵抛物线y=a(x﹣h)2的顶点为P(1,0),
可得y=a(x﹣1)2,
把M(2,2)代入y=a(x﹣1)2得,2=a(2﹣1)2,解得a=2,函数解析式为y=2(x﹣1)2.

练习册系列答案
相关题目