Question

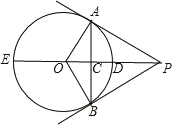
【题目】如图，点E是△ABC的内心，AE的延长线和△ABC的外接圆相交于点D.AD与BC相交于点F，连结BE，DC，已知EF=2，CD=5，则AD=______________.

Answer 1

【答案】

【解析】

根据三角形的内心的定义得到BD=CD，△BDF∽△ADB，根据相似三角形的性质列出比例式，代入计算即可．

∵点E是△ABC的内心，

∴∠BAD=∠CAD，∠ABE=∠CBE，

∴，

∴BD=CD=5，

由圆周角定理得，∠CAD=∠CBD，

∵∠DBE=∠CBD+∠CBE，∠DEB=∠BAD+∠CAD，

∴∠DBE=∠DEB．

∴DE=DB=5，

∴DF=DE-EF=3，

∵∠DBC=∠BAD，∠BDF=∠ADB，

∴△BDF∽△ADB，

∴，

∴AD=，

故答案为：．