题目内容
【题目】△ABC和△DBE是绕点B旋转的两个相似三角形,其中∠ABC与∠DBE、∠A与∠D为对应角.
(1)如图①,若△ABC和△DBE分别是以∠ABC与∠DBE为顶角的等腰直角三角形,且两三角形旋转到使点B、C、D在同一条直线上的位置时,请直接写出线段AD与线段EC的关系;
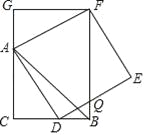
(2)若△ABC和△DBE为含有30°角的直角三角形,且两个三角形旋转到如图②的位置时,试确定线段AD与线段EC的关系,并说明理由;
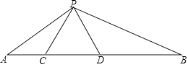
(3)若△ABC和△DBE为如图③的两个三角形,且∠ACB=α,∠BDE=β,在绕点B旋转的过程中,直线AD与EC夹角的度数是否改变?若不改变,直接用含α、β的式子表示夹角的度数;若改变,请说明理由.
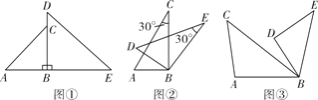
【答案】(1)线段AD与线段CE的关系是AD⊥EC,AD=EC;(2)AD⊥CE,理由详见解析; (3)直线AD与EC夹角的度数不改变,且夹角度数为(180-α-β)度.
【解析】
(1)连接AD、CE,然后证得△ABD≌△BCE,根据所得的等角和等边来判断AD、EC的关系.
(2)连接AD、EC并延长,设交点为点F,根据已知条件,易证得△ABD∽△CBE,得AB:BC=BD:BE,而∠1、∠2同为∠3的余角,则可证得△ABD=△CBE,得∠5=∠7+30°,而∠6=120°-∠5,由此可证得∠7+∠6=90°,即AD⊥CE.
(3)根据上面的求解过程可知:在绕点B旋转的过程中,直线AD与EC夹角的度数不改变,解题思路和方法同(2).
解:(1)线段AD与线段CE的关系是AD⊥EC,AD=EC;
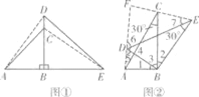
(2)如图②,连接AD、EC并延长,设交点为点F,∵△ABC∽△DBE,∴![]() =
=![]() ,
,
∴![]() =
=![]() .∵∠ABC=∠DBE=90°,∴∠1+∠3=90°,∠2+∠3=90°,∴∠1=∠2,
.∵∠ABC=∠DBE=90°,∴∠1+∠3=90°,∠2+∠3=90°,∴∠1=∠2,
∴△ABD∽△CBE.∴![]() =
=![]() .在Rt△ACB中,∠ACB=30°,tan∠ACB=
.在Rt△ACB中,∠ACB=30°,tan∠ACB=![]() ,∵tan30°=
,∵tan30°=![]() ,∴
,∴![]() .
.
∵∠DBE=90°,∠DEB=30°,∴∠4=60°,∴∠5+∠6=120°.∵△ABD∽△CBE,∴∠5=∠CEB=30°+∠7,∴∠7=∠5-30°,∠6=120°-∠5,∴∠7+∠6=90°,∴∠DFE=90°即AD⊥CE;
(3)在绕点B旋转的过程中,直线AD与EC夹角的度数不改变,且夹角度数为(180-α-β)度

 阅读快车系列答案
阅读快车系列答案