题目内容
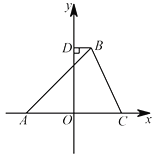
【题目】如图,在平面直角坐标系中,△ABC的顶点A在x轴负半轴上,顶点C在x轴正半轴上,顶点B在第一象限,线段OA,OC的长是一元二次方程x2-12x+36=0的两根,BC=4![]() ,∠BAC=45°.
,∠BAC=45°.
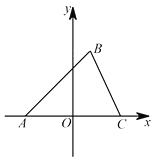
(1)直接写出点A的坐标________点 C的坐标________;
(2)若反比例函数y=![]() 的图象经过点B,求k的值;
的图象经过点B,求k的值;
(3)如图过点B作BD⊥y轴于点D;在y轴上是否存在点P,使以P,B,D为顶点的三角形与以P, O,A为顶点的三角形相似?若存在,直接写出满足条件的点P的坐标;若不存在,请说明理由.
【答案】(1)(-6,0),(6,0);(2)k=16;(3)点P的坐标为:(0,2)或(0,6)或(0,12)或(0,4+2![]() )或(0,4-2
)或(0,4-2![]() ).
).
【解析】
(1)首先利用直接开平方法求出方程 x2-12x+36=0的两根,从而得出OA=OC=6,进而得出A、C两点的坐标;
(2)如图,过点B作BE⊥AC,垂足为E, 根据等腰直角三角形的性质得出AE=BE, 设BE=x,EC=12-x, 在RtΔBEC中利用勾股定理建立方程,求解并检验即可得出BE、OE的长从而得出B点的坐标,然后利用待定系数法即可求出反比例函数的解析式;
(3)存在.如图2,若点P在OD上,若△PDB∽△AOP,根据相似三角形对应边成比例得出![]() ,根据比例式列出方程,求解即可得出P点的坐标;如图3,若点P在OD上方,△PDB∽△AOP, 根据相似三角形对应边成比例得出
,根据比例式列出方程,求解即可得出P点的坐标;如图3,若点P在OD上方,△PDB∽△AOP, 根据相似三角形对应边成比例得出![]() ,则根据比例式列出方程,求解并检验即可得出P点的坐标;如图4,若点P在OD上方,△PDB∽△AOP,根据相似三角形对应边成比例得出
,则根据比例式列出方程,求解并检验即可得出P点的坐标;如图4,若点P在OD上方,△PDB∽△AOP,根据相似三角形对应边成比例得出![]() ,根据比例式列出方程,求解并检验即可得出P点的坐标;如图5,若点P在y轴负半轴,△PDB∽△AOP,根据相似三角形对应边成比例得出
,根据比例式列出方程,求解并检验即可得出P点的坐标;如图5,若点P在y轴负半轴,△PDB∽△AOP,根据相似三角形对应边成比例得出![]() ,根据比例式列出方程,求解并检验即可得出P点的坐标,综上所述即可得出答案.
,根据比例式列出方程,求解并检验即可得出P点的坐标,综上所述即可得出答案.
(1)解一元二次方程 x2-12x+36=0,
解得:x1=x2=6 ,
所以OA=OC=6 ,
故答案为:A(-6,0),C(6,0);
(2)如图,过点B作BE⊥AC,垂足为E,
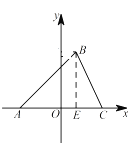
∵∠BAC=45°,
∴AE=BE,
设BE=x,
∵AE+CE=OA+OC=12,
∴EC=12-x,
在RtΔBEC中,BC=![]() ,
,
∴![]() ,
,
整理得:x2-12x+32=0,
解得:x1=4 (不合题意舍去),x2=8,
∴ BE=8,OE=8-6=2,
∴B(2,8),
把B(2,8)代入![]() ,得k=16,
,得k=16,
(3)存在,
如图2,
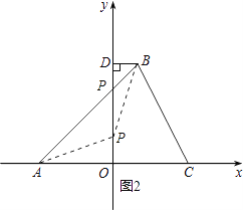
若点P在OD上,若△PDB∽△AOP,
则 ![]() ,即
,即![]() ,
,
解得:OP=2或OP=6,
∴P(0,2)或P(0,6);
如图3,
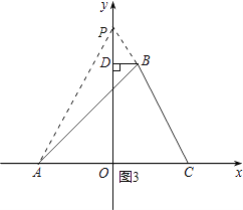
若点P在OD上方,△PDB∽△AOP,
则 ![]() ,即
,即 ![]() ,
,
解得:OP=12,
∴P(0,12);
如图4,
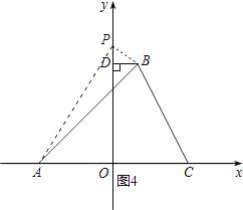
若点P在OD上方,△BDP∽△AOP,
则 ![]() ,即
,即 ![]() ,
,
解得:OP=4+2![]() 或OP=4-2
或OP=4-2![]() (不合题意舍去),
(不合题意舍去),
∴P(0,4+2![]() );
);
如图5,
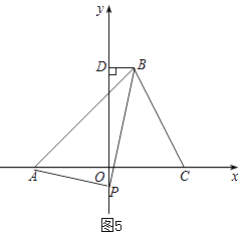
若点P在y轴负半轴,△PDB∽△AOP,
则![]() ,即
,即 ![]() ,
,
解得:OP=-4+2![]() 或-4-2
或-4-2![]() (不合题意舍去),
(不合题意舍去),
则P点坐标为(0,4-2![]() )
)
故点P的坐标为:(0,2)或(0,6)或(0,12)或(0,4+2![]() )或(0,4-2
)或(0,4-2![]() ).
).